Kelvin wakes
The html formatting and custom instructions have been disabled on this server. The same file with adapted formatting can be found here: https://farbeinf.de/static_html/KWake.html.
Watching ducks on a pond one may wonder how these beautiful wake patterns arise.
William Thomson (the famous physicist Lord Kelvin) found already in 1887 the remarkable fact that the angle at which the wake fans out is always the same, regardless whether the wake is caused by a duck, a boat, or a ship, as long as the water is deep as compared with the lengths of the generated waves [1].


| Wakes of ducks on a pond |
Wakes of two boats on Avon Gorge.
Photo: Arpingstone, source |
While the mathematical treatment of water waves is difficult, see the Wikipedia article, some results are easy to obtain, and in particular the shape of the wake can be explained using only elementary maths [2].
Whereas sound waves propagate with the same velocity irrespective of their length, with the well known effect of shock waves when flying objects exceed sound velocity, in deep water the velocity of the waves depends on the wavelength. The longer the waves, the faster they propagate. This can be found from a simple dimensional analysis.
What are the quantities on which the velocity of the waves may depend? Clearly the wavelength λ, the depth of the water H, the earths gravitation g, the density of the water ρ, the surface tension σ, or what else? The surface tension affects only very short waves, here we may ignore it. If the water is deep, so to say infinitely deep, the depth cannot occur in an expression for the wave velocity.
If we have an equation like
v = something,
then this “something” must have the dimension of a velocity, i.e. length divided by time. The square root of wavelength times gravitational acceleration has this dimension, thus we conclude that the velocity is proportional to this root:
v ∝ √gλ .
(The exact expression for the phase velocity is
vφ = √gλ ⁄ (2π) .)
The phase velocity is, roughly speaking, the velocity of the individual wave crests. A wave train of finite length, however, moves with the group velocity which in this case is only half the phase velocity, vg = vφ/2. (This follows from the above equation and the general expression for the group velocity, see e.g. this Wikipedia article.) If we look at a group of waves, following a particular crest, we see that it moves forward faster than the whole bunch, gets weaker as it approaches its front, and vanishes. But from behind, a new crest comes up, gets stronger, and weaker again as it approaches the leading edge …
The phase velocity of gravity waves depends on the wavelength and the group velocity is half the phase velocity, that is all what is necessary to understand the gross features of the wakes.

|
Let us first consider the fictitious case where groups and phases travel with the same speed, which we assume to be 80 % of that of the boat. This is sketched to the left. The boat continuously produces waves. We invoke Huygens' principle to find the resulting shock wave. The circles are the elementary waves emitted at the points marked by dots along the boat's trajectory. At the envelope of all the circles the wavelets have all the same phase and interfere constructively which yields the resulting wave front, whereas at all other places the wavelets almost cancel each other.
|

|
Next we assume that the boat excites real water waves. We consider a single frequency out of the whole spectrum.
Instead of forming a shock wave, the wavelets produced earlier have only travelled half the way and thus the angle which the wake encloses with the path line of the boat is smaller and can easily be found graphically.
|
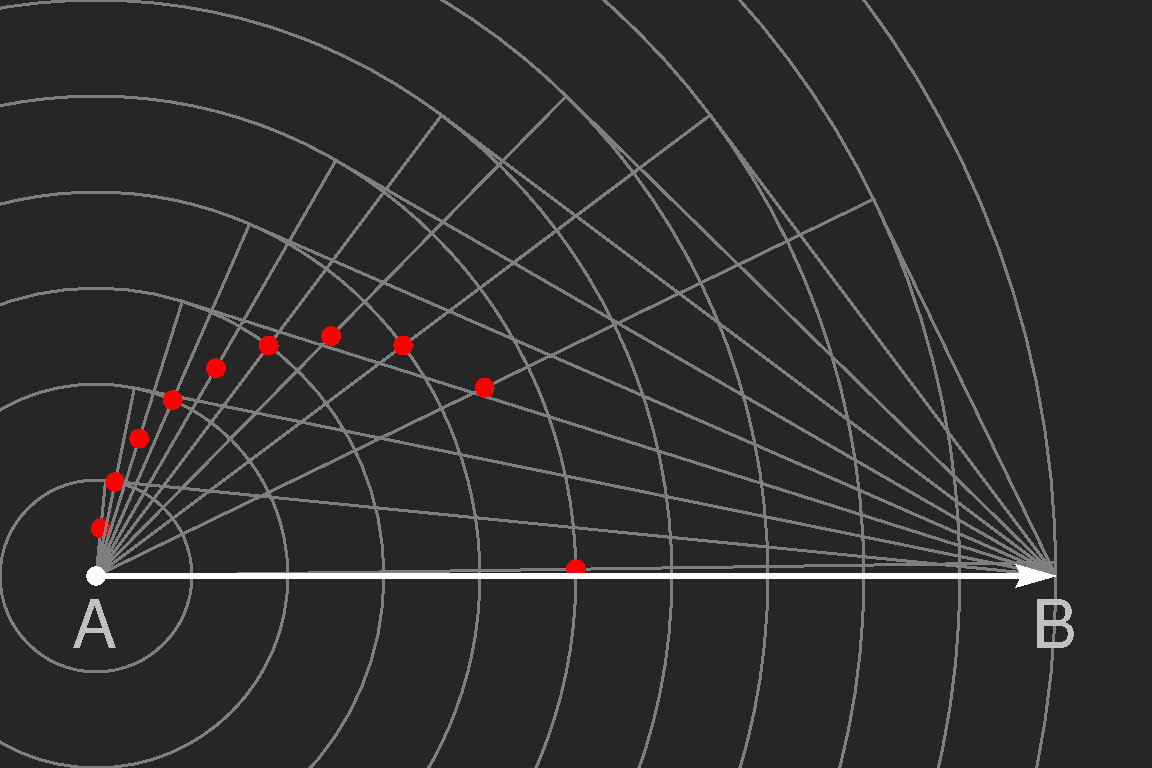
| The boat excites waves of all possible wavelengths and corresponding phase and group velocities, and in the left figure the construction of the wake angles for phase velocities of 10, 20, 30 … 99.99 percent of the boat's speed is shown. The red dots mark the points where the waves emitted at point A have arrived when the boat is at point B. From the construction it is clear that the red dots are lying on a circle with radius one quarter of the distance AB. Note that the waves with phase velocity equal to the boat's speed follow the boat along its path with wake angle of 0°.
|
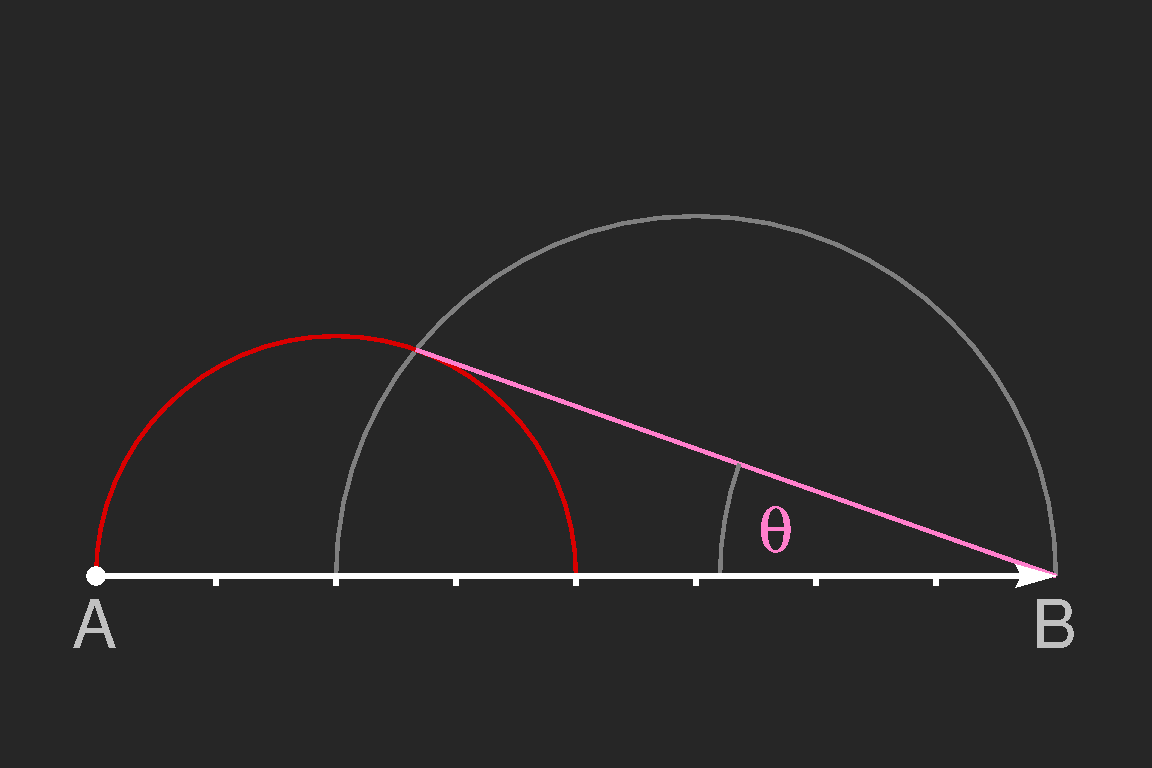
| We can easily determine the maximum angle θ of possible wakes. The direction of the wake is given by the tangent to the red circle drawn from point B. Along this line the crests of the waves are highest, the troughs deepest, as all the wavelets in the neighbourhood of wavelengths interfere constructively. From the sketch it is seen that sin(θ) = 1/3, and thus θ = 19.47°. This has been found by William Thomson, and it is true as long as the group velocity is half the phase velocity.
|

|
The waves with phase velocity equal or close to the boat's (or duck's) speed follow the boat (or duck) along its path with zero or small wake angle and form the trail of transverse waves. The whole pattern seems to be rigidly fixed to the boat if that moves straightforward with constant speed. |
Strongly powered fast boats apparently arouse narrower wakes. This has been discussed recently by Rabaud and Moisy [3], see also [4], [5] and is due to the fact that waves longer than the boat's hull are excited the less the longer they are.
[1] William Thomson (1887): "On ship waves", Institution of Mechanical Engineers, Proceedings, 38:409–434 pp. 641–649.
[2] Frank S. Crawford: Elementary derivation of the wake pattern of a boat. Am. J. Phys. 52, 782 (1984); (abstract).
[3] Marc Rabaud and Frédéric Moisy: Ship wakes: Kelvin or Mach angle? arXiv.org > physics > arXiv:1304.2653 or
PRL
110,
214503 (2013)
[4] Lord Kelvin Wipes Out on Speed Boat Wakes?
By Adrian Cho, May 9, 2013 link
[5] Reawakening the Kelvin wake. By Hamish Johnston
link
Legal Information Data Privacy






