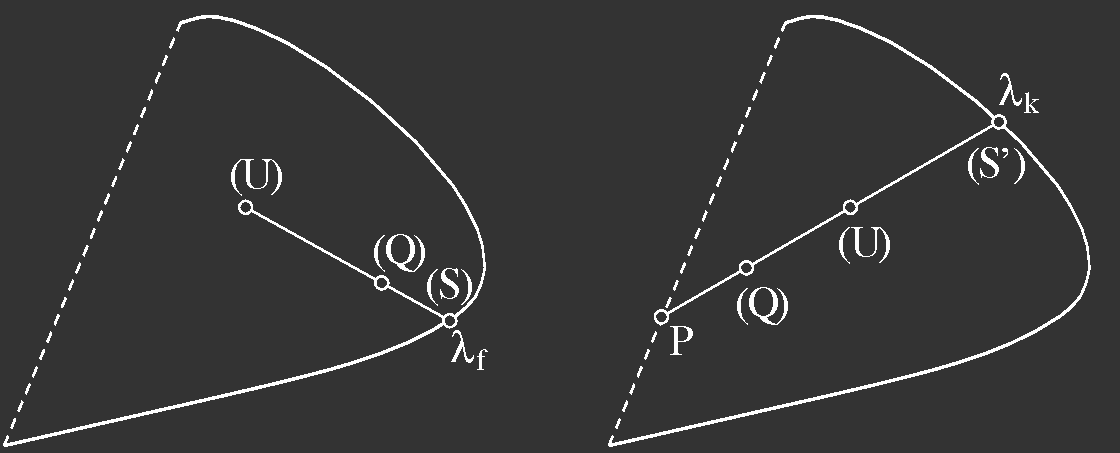Farbmetrik
Die html-Formatierung und benutzerdefinierte Anweisungen wurden auf diesem Server deaktiviert. Die gleiche Datei mit angepasster Formatierung finden Sie hier: https://farbeinf.de/static_html/fmetr.html.
Hier sollen die Konzepte der Farbmessung und -Berechnung eingeführt
werden. Die hier besprochenen Zusammenhänge, die zur Messung und
Kennzeichnung von Farben verwendet werden, gehören zum wichtigsten
experimentellen Material über unseren Gesichtssinn, denn die Eigenschaften
des Auges sind naturgemäß die Grundlage der Farbmessung.
Grundlagen der Farbenmessung
Das von einem Gegenstand reflektierte, durchgelassene oder von ihm
selbst ausgesandte Licht, das ins Auge eintritt und eine Farbempfindung
hervorruft, ist der Farbreiz. Zwar nehmen wir außer der Farbe
auch noch wahr, ob der Gegenstand selbst leuchtet oder beleuchtet
ist, ob er transparent oder lichtundurchlässig ist; wir bemerken, ob
die Oberfläche matt oder glänzend ist, und dabei können verschiedene Arten Glanz unterschieden werden (Glasglanz, Metallglanz), aber
man kann sich leicht überzeugen, dass all diese Attribute außer Farbe
und Helligkeit nur durch das Zusammenwirken der Eindrücke von benachbarten Stellen des Gegenstandes und seiner Umgebung bestimmt
werden: Betrachtet man eine Stelle, die so klein ist, dass sie völlig
einheitlich erscheint, durch eine Blende, so bleiben nur die Merkmale
Farbe und Helligkeit übrig.
Das Licht, also der Farbreiz, kann mit physikalischen Mitteln untersucht
werden: Es kann durch ein Prisma in Anteile verschiedener Wellenlängen
aufgespalten werden, und man kann messen, welche Energie
pro Zeiteinheit in einem bestimmten Wellenlängenbereich transportiert wird.
Man unterteilt die Wellenlängenskala in kleine Abschnitte. Die Leistung (Energie/Zeiteinheit), die von der Strahlung in so einem kleinen
Wellenlängenbereich in dem Intervall von λ − Δλ/2 bis λ + Δλ/2
in einen bestimmten Raumwinkelbereich hinein (z. B. in die Pupille)
transportiert wird, nennen wir
φλΔλ (1)
(Diese Leistung ist natürlich umso größer, je größer Δλ gewählt wird,
daher schreiben wir Δλ als Faktor dazu.)
Kennen wir φλ für alle Wellenlängen des sichtbaren Bereiches, also
für jeden Abschnitt der Wellenlängenskala, so haben wir eine Funktion
der Wellenlänge vorliegen, die spektrale Leistungsverteilung, die von
der Physik her den Farbreiz vollständig bestimmt. Man nennt φλ auch
Farbreizfunktion.
Wir stellen fest, dass z. B. eine Verdopplung der Werte φλ für alle
Wellenlängen zwar die Helligkeit, nicht aber die Farbe einer Strahlungsquelle
ändert; daher ist es üblich, diese Funktion willkürlich zu
normieren, d.h. mit einem beliebigen Zahlenfaktor zu multiplizieren,
so dass man die Funktionen für Lichtquellen verschiedener Strahlungsleistung
bequem in einem Diagramm unterbringen kann. (Noch größere Bequemlichkeit
bedeutet dies für die Messung, da man sich auf
eine Relativmessung beschränken kann, die viel einfacher ist als eine
Absolutmessung).
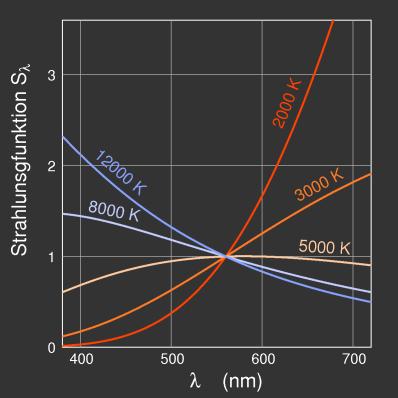
Bild 1: Strahlungsfunktion des Schwarzen Körpers bei verschiedenen
Temperaturen. Die Kurven geben die relative Strahlungsleistung in
den verschiedenen Wellenlängenbereichen an. Durch die willkürliche
Festlegung des Wertes für 560 nm auf 1 sind die Kurven in vergleichbare Größenordnung gebracht; tatsächlich nimmt die Strahlungsleistung in jedem Wellenlängenbereich mit der Temperatur zu; die Absolutwerte
für 2000 K liegen überall unter denen für 12000 K
Abb. 1 zeigt Beispiele solcher Farbreizfunktionen.
Hat man Licht durch ein Prisma in seine Anteile verschiedener
Wellenlängen zerlegt, so kann man es auch wieder vereinigen und feststellen,
dass es sich in der Farbe nicht von dem ursprünglichen unterscheidet.
Man kann daher das Licht immer als Summe der Anteile
der verschiedenen Wellenlängen auffassen, und die Farbreizfunktion
φλ gibt an, welche Mengen aus dem jeweils betrachteten kleinen Wellenlängenbereich benötigt werden.
Falls die untersuchte Strahlung direkt von einer Lichtquelle stammt,
schreiben wir statt φλ lieber Sλ und nennen Sλ die Strahlungsfunktion der Lichtquelle.
Die naheliegende Vermutung, dass durch φλ auch der Farbeindruck bestimmt ist, ist schnell widerlegt: durch Kontrast zur Umgebung, Anpassung des Auges an die herrschende Beleuchtung und
nicht zuletzt durch die Verarbeitung der Daten im Gehirn sind erhebliche
Unterschiede in der Farbempfindung möglich. Ein gutes Beispiel
dafür ist die schlagartige scheinbare Veränderung des grauen Himmels,
wenn am Abend die elektrische Beleuchtung eingeschaltet wird.
Ebenfalls sehr deutlich lässt sich diese Kontrastwirkung am Beispiel
der
"Farbigen Schatten" leicht experimentell demonstrieren.
Dazu braucht man zwei verschiedene Lichtquellen, z. B. einen Projektor mit Rotfilter und einen ohne Filter, mit denen man eine weiße
Leinwand beleuchtet. Jeder Schatten eines vor die Leinwand gehaltenen Gegenstandes erscheint nun doppelt: der nur von Rotlicht beleuchtete wie zu erwarten rot, aber der von Lampenlicht erleuchtete
erscheint nicht weiß, sondern bläulich-grünlich. Dieser Versuch, mit
einer Kerze in der Dämmerung ausgeführt, wurde zuerst von Otto v.
Guericke im Jahre 1672 beschrieben (Land 1977). E. H. Land gibt in
der zitierten Arbeit Experimente mit größerem technischen Aufwand
in, die die Variabilität der Farbempfindung bei gleichbleibendem Farbreiz noch deutlicher machen.
Aber nicht nur durch gleichzeitig sichtbare verschiedene Farbreize,
sondern auch durch die zeitliche Aufeinanderfolge kommt es zu Kontrastwirkung, da die Beeinflussung des Auges einige Zeit nachwirkt.
Zumal sich Farbempfindungen ohnehin nicht (oder noch nicht)
messen lassen, schaltet man sie bei der Farbmessung völlig aus, indem man nur nach der Unterscheidbarkeit oder Ununterscheidbarkeit
eines Farbreizes von einem vorgegebenen anderen fragt und nicht nach
dem Eindruck, den er hervorruft.
Damit die Form der Gegenstände und deren Umgebung den Beobachter nicht unbewusst beeinflusst, und um die Vergleichbarkeit optimal zu machen, werden die zu vergleichenden Farbreize als
"freie
Farben" in den Hälften einer kreisförmigen Blende bestimmter Öffnung dargeboten (Aperturfarben), die Blende bietet den Anblick einer selbstleuchtenden Öffnung ohne Struktur. Besonders zur Untersuchung farbiger Oberflächen geeignet ist die
"Maxwellsche Beobachtungsweise": Wenn man etwas mit einer Lupe betrachtet, dann kann
man die Abstände so wählen, dass die ganze Fläche der Lupe einheitlich
farbig erscheint.
Bei der Farbe, die so losgelöst vom Gegenstand erscheint, ist nun
auch eine Trennung von Gegenstands"Farbe" und Beleuchtungseinfluss nicht mehr möglich, die sonst zumeist unbewusst und mit erstaunlicher Genauigkeit vorgenommen wird, und das Experiment reduziert
sich auf den Vergleich zweier durch ihre spektralen Verteilungen gegebener Lichtströme, zweier Farbreize.
Stimmen zwei Farbreize in ihren spektralen Verteilungen überein,
also φ1,λ = φ2,λ, so erscheinen sie unbedingt gleich, man spricht in diesem Fall von Isomerie. Die Farbreize können aber auch gleich erscheinen, wenn die Verteilungsfunktionen verschieden sind. Diese Übereinstimmung nennt man Metamerie oder bedingte Gleichheit.
Um diesem Sachverhalt Rechnung zu tragen, führen wir die Wertigkeit V eines Farbreizes in Hinblick auf den Farbsinn des Beobachters
ein. Erscheinen einem Beobachter zwei Farbreize gleich, so schreiben
wir
V1 = V2 (2)
d.h. die Wertigkeiten, Farbvalenzen oder kurz Valenzen der beiden
Farbreize sind gleich, und über die Farbreizfunktion selbst sagt diese
Gleichung nichts aus. Obwohl farbtüchtige Beobachter in ihren Urteilen im großen und ganzen übereinstimmen, gilt die Gleichung streng
genommen zunächst nur in Hinblick auf den einen Beobachter.
Betrachten wir eine Versuchsanordnung: die linke Hälfte einer Projektionsleinwand soll von einer Lampe durch ein Farbfilter beleuchtet
werden, und diese Farbe soll auf der rechten Hälfte reproduziert werden. Dazu stehen drei Projektoren mit Farbfiltern zur Verfügung, deren Helligkeit regelbar ist. Durch Überlagerung (Addition) der drei
Farbreize mit verschiedenen Gewichten kann man Mischfarben erzeugen. Wählt man als Basisvalenzen Rot, Grün und Blau, alle drei
möglichst gesättigt, kann man in vielen Fällen Übereinstimmung erreichen. Das heißt, und dies ist eine fundamentale experimentelle Erkenntnis, die Farben (alle Farbtöne!) können als Mischung aus drei
verschiedenen, fest vorgegebenen Farbreizen dargestellt werden. Dabei
ist es aber durchaus möglich, dass ein zweiter Betrachter Übereinstimmung bei einer vom ersten etwas abweichenden Einstellung feststellt,
usw. Wir schreiben die Übereinstimmung der Bildhälften als Gleichung
für die Farbvalenzen:
V = RR + GG + BB (3)
Die fett gedruckten Großbuchstaben stehen für Farbvalenzen, die Buchstaben R, G, B (Farbmaßzahlen) für die in zunächst noch beliebigen
Einheiten gemessenen Mengen der Grundvalenzen R, G, B.
Es kann allerdings vorkommen, z.B. wenn als Probelichtquelle eine
spektral reine oder eine sehr intensive Farbe genommen wird, dass mit
der gegebenen Anordnung keine Anpassung der beiden Felder aneinander erreicht werden kann, dass etwa ein tiefes Dunkelrot aus Orangerot,
Grün und Blau nicht gemischt werden kann, die Mischfarbe immer etwas weißlicher erscheint. Wenn der Farbvergleich der Messung und
nicht der Reproduktion dient, kann man sich in diesem Fall behelfen,
indem man etwa die grüne Lichtquelle in der Versuchsanordnung auf
die andere Seite nimmt. Wenn dann Gleichheit erreicht werden kann,
entsprechend
V + GG = RR + BB (4)
so können wir dies schreiben als
V = RR − GG + BB; (5)
wobei jetzt negative Mengen eines Farbreizes auftreten. Für eine praktische Realisierung einer Farbwertgleichung sind die Terme so umzustellen, dass nur positive Gewichtsfaktoren auftreten, und den beiden
Seiten der Gleichung entsprechen dann mögliche Beleuchtungen der
beiden Bildfeldhälften.
Lässt man negative Beimischungen zu, dann gilt Gleichung (3) allgemein unter der Voraussetzung, dass nicht eine der drei Vergleichsfarben durch die beiden anderen nachgemischt werden kann. Dies ist das 1. Graßmannsche Gesetz, das man so formulieren kann: Von vier
Farben lässt sich immer eine als Überlagerung der anderen darstellen.
Weiters stellt man fest: Hat man eine metamere Übereinstimmung,
so bleibt diese Übereinstimmung erhalten, wenn die Helligkeit von
beiden im gleichen Maße erhöht oder verringert wird, es gilt also
V1 = V2 ⇒ aV1 = aV2 (6)
zumindest innerhalb gewisser Grenzen. (Wenn man die Helligkeit soweit vermindert, dass man in den Bereich des Dämmerungssehens kommt,
kann die Übereinstimmung aufhören.)
Die Gleichheit zweier Farben bleibt auch bestehen, wenn beiden
die gleiche Farbe additiv überlagert wird:
V1 = V2 ⇒ V1 + U = V2 + U (7)
oder auch
U1 = U2, V1 = V2 ⇒ U1 + V1 = U2 + V2 (8)
(3. Graßmannsches Gesetz, H. Graßmann 1853)
Haben wir für V1, V2 die Maßzahlen R1, G1, B1 bzw. R2, G2, B2
ermittelt,
V1 = R1R + G1G + B1B
V2 = R2R + G2G + B2B (9)
dann gilt auch
V1 + V2 = (R1 + R2) R + (G1 + G2) G + (B1 + B2) B. (10)
Es besteht also ein linearer Zusammenhang zwischen den Farbreizen
und den Farbmaßzahlen, und es gelten für die Addition von metameren
Farbvalenzen die gleichen Gesetze wie für die Addition von Vektoren. Daher kann man jeden Farbwert als Vektor in einem Farbenraum darstellen, und dieser Farbenraum ist dreidimensional, d. h. es gibt nur
drei linear unabhängige Basisvektoren, genau wie in dem physikalischen Raum unserer Anschauung. Damit haben wir die Dreidimensionalität des Farb-Empfindungs-Raumes in der Dreidimensionalität des
Raumes der Farbwerte wiedergefunden.
In der Darstellung durch Vektoren unterscheiden sich Farben, die
durch Vektoren in der gleichen Richtung gegeben sind, nur durch ihre Helligkeit; die Farbart ist allein durch die Richtung des Vektors
gegeben.
Bis jetzt ist nichts über die Einheiten gesagt worden, in denen die
Farbvalenzen gemessen werden; man kann sie willkürlich festlegen. Es
ist üblich, diese Festlegung wie folgt zu treffen: Je eine drittel Einheit
der Primärvalenzen Rot, Grün und Blau (Blauviolett) addiert sollen
eine Einheit Weiß ergeben, wobei als Weiß die Farbvalenz des energiegleichen Spektrums φλ = const gewählt wird. Die absolute Größe der
Einheiten ist wegen Gl. (6) unerheblich, es wird auf diese Weise nur
die relative Größe fixiert.
1/3 (R + G + B) = E
(11)
Die in diesen Einheiten gemessenen Größen R, G, B nennt man die
trichromatischen Maßzahlen.
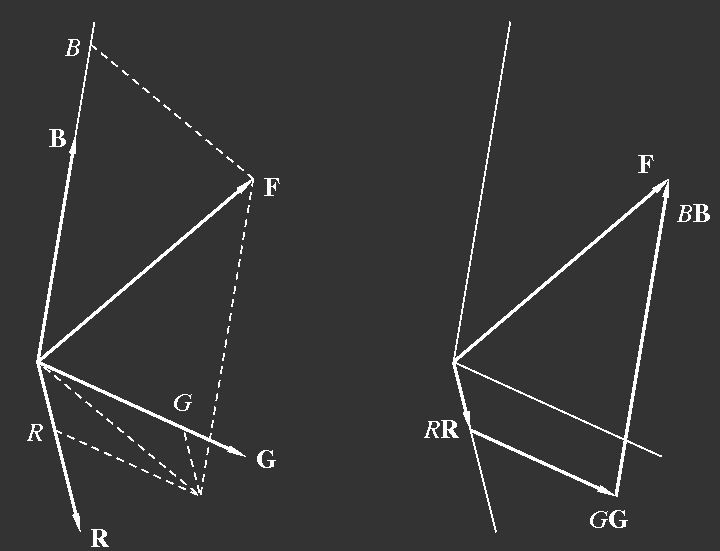
Bild 2: Darstellung eines Farbvektors
F als Summe dreier Komponenten.
R,
G,
B sind Einheitsvektoren,
RR etc. dann Vektoren in
Richtung der Einheitsvektoren, aber mit veränderter Länge.
F ist die
vektorielle Summe von
RR,
GG und
BB. Dies ist in der Abbildung
rechts noch einmal hervorgehoben. In diesen Skizzen sind
R, G, B
die Beträge der Komponenten,
RR,
GG und
BB die Komponentenvektoren
Das für die additive Farbmischung maßgebliche Gewicht einer Farbvalenz, die Zahl der trichromatischen Einheiten, erhält man als Summe
der Gewichte der Komponenten: Zwei Einheiten der Farbe A plus drei
Einheiten der Farbe B ergeben fünf Einheiten der Mischfarbe.
Die Farbvalenzvektoren haben nicht alle Eigenschaften, die wir
sonst von Vektoren kennen. Für unsere Zwecke hier reicht die Vorstellung von einem Pfeil mit Spitze, Ende und bestimmter Länge, wobei
die Addition erfolgt, indem man einen parallelverschiebt und mit dem
Ende auf die Sitze des ersten aufsetzt. Dies ist so wie beim Hintereinanderausführen von Verschiebungen eines Punktes. Multiplikation mit
einer Zahl bedeutet Multiplikation der Länge unter Beibehaltung der
Richtung, bei Multiplikation mit einer negativen Zahl dreht sich die
Richtung um. Dabei hat aber die Länge der Valenzvektoren selbst keine tiefere Bedeutung, sondern als Maß für das Gewicht der Valenzen
bei Farbmischungen dient die Summe ihrer Komponenten, eine Größe,
der sonst bei Vektoren keine Bedeutung zukommt. Im Farbraum liegen die Spitzen aller Vektoren einer bestimmten Einheitenzahl m in
der Ebene R + G + B = m.
Da die Helligkeit vielfach weniger interessiert als die Farbart, geht
man von der dreidimensionalen Darstellung zur einfacheren zweidimensionalen über, indem man als Farbdiagramm die Einheitsebene
R+G+B = 1 zeichnet, wobei die Farbart durch die Durchstoßpunkte
der Farbvalenzvektoren gegeben ist. (Die Abbildungen 3 zeigen den
Zusammenhang.)
Aus R, G, B berechnet man die Koordinaten des Durchstoßpunktes
zu
r =
R/(R + G + B), g =
G/(R + G + B), b =
B/(R + G + B)
(12)
und es ist natürlich r + g + b = 1, so dass nur zwei der Koordinaten
(Farbwertanteile) angegeben werden müssen. Für einen eingezeichneten Punkt lassen sich diese Koordinaten unmittelbar dem Farbdreieck
entnehmen als Abstände des Punktes von den Dreiecksseiten, wobei
die Einheiten durch die jeweilige Höhe des Dreiecks gegeben sind (z.B.
g = (Abstand F–V)/HG).
Die Form des Dreiecks ist im übrigen willkürlich; da auch die Winkel zwischen den Achsen in Abb. 3 keine Bedeutung haben, kann man
das Farbdreieck rechtwinklig oder gleichseitig zeichnen, ohne an den
obigen Beziehungen etwas zu ändern.
Aus der Konstruktion folgt, dass die Überlagerung zweier Farben
im Farbdreieck durch einen Punkt auf der Verbindungslinie der beiden Ausgangsfarbarten dargestellt wird, und die Abstände verhalten
sich umgekehrt wie die Mengen (in trichromatischen Einheiten) der
Komponenten (Hebelgesetz), Abb. 4.
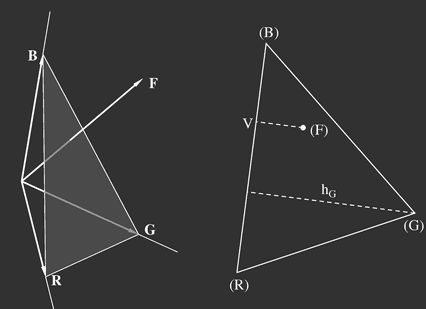
Bild 3: Links: Das Farbdreieck im Farbraum: Die Farbart der als Vektorpfeil eingezeichneten Farbvalenz ist durch den Durchstoßpunkt des
Farbvektors durch die Einheitsebene gegeben. Rechts: Die Einheitsebene mit dem eingezeichneten Durchstoßpunkt (F) der Farbvalenz
F.
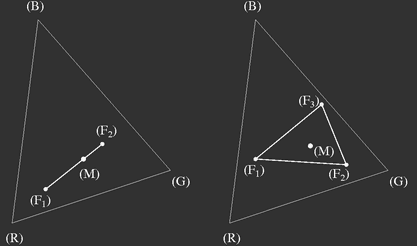
Bild 4: Für die additive Mischung von Farben gilt im Farbdreieck der
Hebel- oder Schwerpunktssatz: Denkt man sich an den Farborten Gewichte angebracht, die durch die Einheitenzahlen der Farben
F1,
F2,
… gegeben sind, so befindet sich der Farbartpunkt der Mischfarbe
genau im gemeinsamen Schwerpunkt dieser Gewichte.
Bemerkenswert ist der Helligkeitsunterschied der Primärvalenzen
R, G, B. Bei Verwendung von spektralreinem Licht der Wellenlängen
λR = 700 nm, λG = 546,1 nm, λB = 435,8 nm für die primären
Farbreize erscheint eine Einheit Rot etwa 15 bis 20 mal so hell wie
eine Einheit Blau, eine Einheit Grün noch vier bis fünf mal so hell wie Rot, d. h. etwa viereinhalb Einheiten R erscheinen erst so hell wie G.
Allerdings ist der Vergleich der Helligkeiten von verschiedenen Farben
problematisch, und so sind die den genormten Lichtquellen zugeordneten Helligkeitsbeiwerte (Leuchtdichtebeiwerte) als aus der Helligkeitsempfindungskurve Vλ entnommene Zahlen und nicht als mit derart
exzessiver Genauigkeit gemessene Werte zu verstehen. Die Helligkeitsempfindungskurve Vλ ist aus Messreihen an einer größeren Zahl von
farbnormalsichtigen Versuchspersonen gewonnen worden und kann als
repräsentativ gelten (
"Normalbeobachter"). Für die oben angegebenen Wellenlängen sind die Leuchtdichtebeiwerte
lR = 1, lG = 4,5907; lB = 0,0601 (13)
damit errechnet man die Helligkeit (Leuchtdichte) eines farbigen Lichtes zu
cL = lRR + lGG + lBB (14)
Dabei ist c ein Proportionalitätsfaktor, über den wir noch so verfügen
können, dass sich L in den gewünschten Einheiten ergibt, z. B. in
cd/m2, Candela pro Quadratmeter.
Diese Beziehung beruht auf der Voraussetzung, dass sich die Helligkeiten additiv verhalten (Abneysches Gesetz), dies gehört gleichsam
zur Definition der Helligkeit.
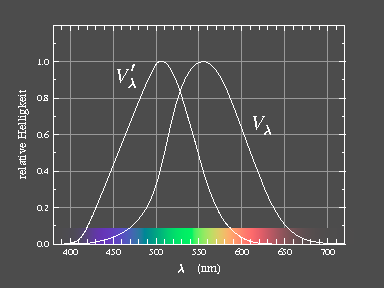
| 
| Bild 5: Relative Empfindlichkeit als Funktion der Wellenlänge: V'λ für skotopisches (Nacht-), Vλ für photopisches (Tages-) Sehen. |
Bemerkenswert ist im übrigen, dass die Energien, die die drei Lichtquellen je Zeiteinheit aussenden, wieder in einem anderen Verhältnis
stehen: Es ist, für je eine trichromatische Einheit
SR : SG : SB = 72,0962 : 1,3791 : 1 (15)
Berechnung der Farbmaßzahlen
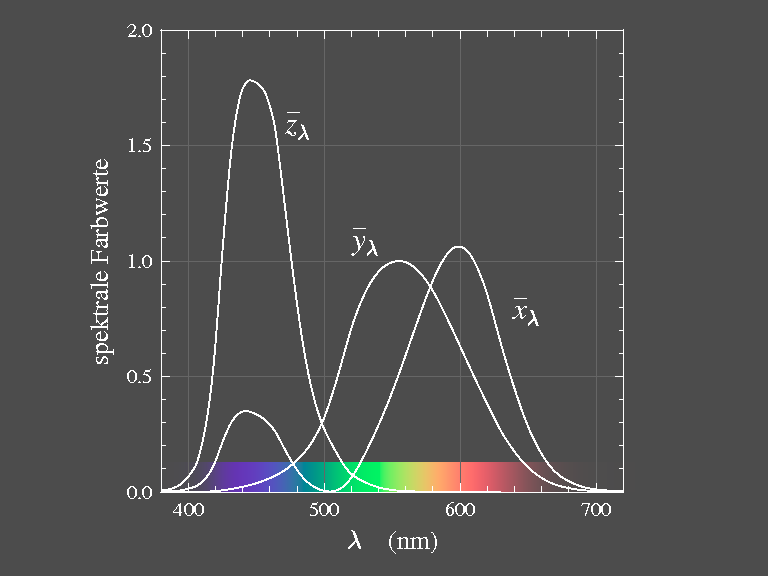
Die trichromatischen Maßzahlen für spektralreines Licht sind von besonderer Bedeutung: Für Strahlung der Wellenlängen λ (Farbreiz qλ)
erhält man die Maßzahlen ‾rλ, ‾gλ, ‾bλ, die spektrale Farbwerte genannt werden. Variiert man λ, wobei die Strahlungsintensität festgehalten wird oder auf eine Einheit (z. B. 1 Watt/m2) zurückgerechnet
wird, dann stellen ‾rλ, ‾gλ und ‾bλ Funktionen von λ dar, die Spektralwertkurven (Abb. 6). Sind die Spektralwertkurven bekannt, dann
kann man die Farbmaßzahlen für einen durch die Funktion φλ bestimmten Farbreiz berechnen.
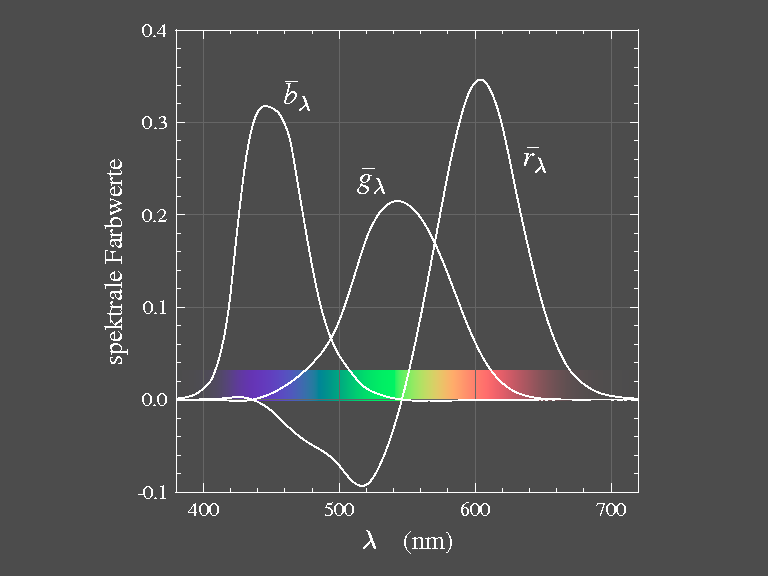
| 
| Bild 6: Die Farbwerte der Spektralfarben für reelle, spektralreine
Grundfarben (nach DIN 5033): λR = 700 nm, λG = 546,1 nm,
λB = 435,8 nm. |
Dazu denken wir uns den sichtbaren Wellenlängenbereich wieder
in kleine Intervalle der Größe Δλ zerlegt. Wäre die Intensität in einem
herausgegriffenen Teilbereich eine Einheit groß, so wären die trichromatischen Koordinaten für diesen Teilbereich ‾rλ, ‾gλ,‾bλ. Die Maßzahlen
für einen Teilbereich der Intensität φλΔλ sind daher
‾rλφλΔλ, ‾gλφλΔλ, ‾bλφλΔλ. (16)
Nun haben wir über alle Teilbereiche aufzusummieren und erhalten
R =
∑λ‾rλφλΔλ,
G =
∑λ‾gλφλΔλ,
B =
∑λ‾bλφλΔλ. (17)
Die Durchstoßpunkte durch die Einheitsebene für die Spektralfarben berechnet man nach Gl. (12) zu
rλ =
‾rλ/(‾rλ + ‾gλ +‾bλ),
gλ =
‾gλ/(‾rλ + ‾gλ +‾bλ),
bλ =
‾bλ/(‾rλ + ‾gλ +‾bλ). (18)
Trägt man diese Punkte für alle Wellenlängen des sichtbaren Bereiches
in die Farbtafel ein, so erhält man den Spektralfarbenzug Abb. 7. Die
Größen rλ, gλ und bλ sind die Farbwertanteile der Spektralfarben, kurz
Spektralwertanteile.
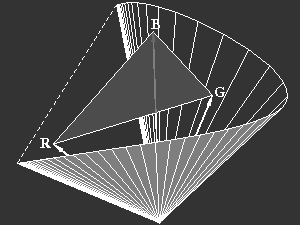
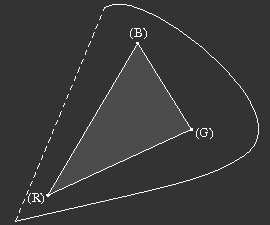
Bild 7: Links: Die Farbvalenzvektoren der Spektralfarben bilden in ihrer Gesamtheit eine Art Tüte im Farbraum. Alle realisierbaren Farben liegen innerhalb dieser Farbtüte. Rechts: "Ins" Farbdreieck eingetragen, ergeben die Farbartpunkte
der Spektralfarben den Spektralfarbenzug, das ist die Schnittkurve der Spektralfarbtüte mit der Einheitsebene. Die Verbindungslinie des lang- und kurzwelligen
Endes des Spektralfarbenzuges ist die Purpurlinie. Innerhalb des so abgeschlossenen Gebietes liegen alle überhaupt möglichen Farbarten.
Es liegt auf der Hand, dass bei der Mischung von Spektralfarben aus
vorgegebenen Primärvalenzen nur die verallgemeinerte Form der Gleichung (3) mit einem oder auch zwei negativen Koeffzienten möglich
ist, denn Spektralfarben sind die sattesten Farben überhaupt. Daher
liegt der Kurvenzug der Spektralfarben außerhalb des Dreiecks unserer Primärvalenzen. Die Kurve ist nicht geschlossen. Beim Mischen der
Valenzen von den beiden Endpunkten bewegen wir uns auf der Purpurlinie, der Verbindungslinie der Endpunkte. Alle überhaupt möglichen
Farbvalenzen befinden sich in der Farbtafel innerhalb des durch die
Purpurlinie geschlossenen Spektralfarbenzuges.
Der in die Farbtafel eingezeichnete Spektralfarbenzug ermöglicht
die Angabe einer anderen Charakterisierung der Farbvalenz Q, die auf
Helmholtz zurückgeht und den psychologischen Begriffen Farbton und
Sättigung entspricht (Abb. 8): Man legt eine unbunte Farbe U fest,
und zeichnet eine Gerade durch die Punkte (Q) und (U), die bis zum
Spektralfarbzug zu ziehen ist. Zwei Fälle lassen sich unterscheiden:
Liegt (Q) zwischen (U) und (S), so lässt sich Q aus U und spektralreinem Licht der Wellenlänge λS mischen, man nennt λf = λS die
farbtongleiche Wellenlänge. Oder aber es liegt (U) zwischen (Q) und
(S), dann kann die unbunte Farbe U (Weiß) durch Q und spektralreines Licht der Wellenlänge λS' gemischt werden. Man nennt λk = λS
die kompensative Wellenlänge. Als Sättigung bezeichnet man im ersten Fall den Anteil an der Spektralfarbe, der für die Mischung nötig
wäre und der durch das Streckenverhältnis
pQ = (QU)/(SU) (19)
gegeben ist, im zweiten Fall bezeichnet Sättigung den Anteil, der von
einem auf der Purpurlinie gelegenem Farbreiz benötigt würde, um Q
aus U und P zu mischen, und der ist durch das Streckenverhältnis
pQ = (QU)/(PU)(20)
gegeben. Die DIN-Norm (DIN 5033) zieht statt des Ausdruckes Sättigung die Bezeichnung spektraler Farbanteil bzw. bei Selbstleuchtern
spektraler Leuchtdichteanteil vor.
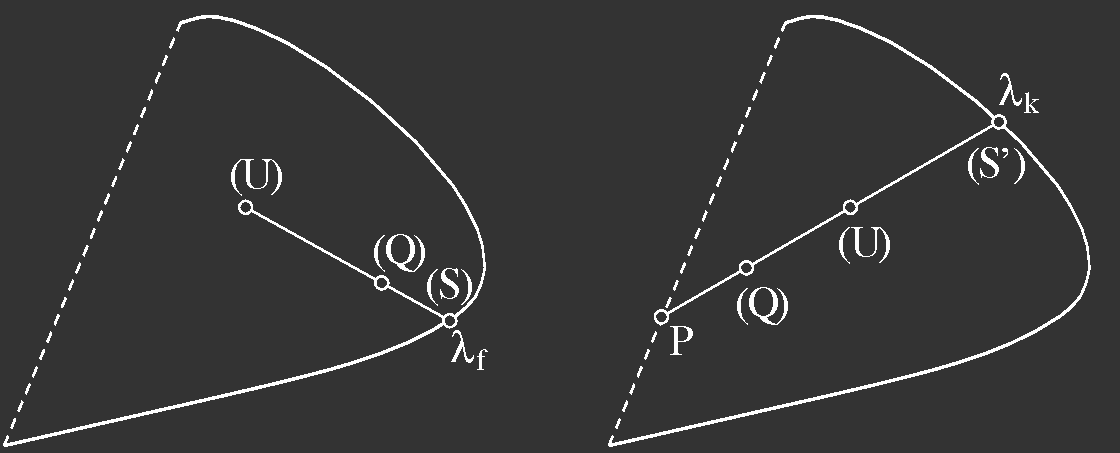
Bild 8: Zur Bestimmung der Helmholtz-Maßzahlen
Statt kompensative Wellenlänge könnte man ebensogut komplementäre Wellenlänge sagen, wie es in der angelsächsischen Literatur
auch geschieht. Der Wortbedeutung nach sagen beide Ausdrücke etwa
dasselbe: die vorgegebene Farbe wird mit der kompensativen zu Unbunt gemischt,
"ausgeglichen", oder mit der komplementären zu Weiß
"aufgefüllt". Komplementär wird bisweilen in Hinblick auf die Farbreizfunktion verstanden – zwei Farbreize sind komplementär, wenn
sie additiv die vorgegebene Farbreizfunktion von Unbunt ergeben. Da
aber in der Farbmessung im allgemeinen von Farbvalenzen die Rede
ist, wird unter Komplementärfarben im folgenden ein Paar verstanden,
das sich in irgend einem Verhältnis additiv zu Weiß mischen lässt.
Die Wahl anderer Primärfarben
Es ist leicht, von einem Satz Primärvalenzen auf einen anderen unzurechnen, was z. B. für den Vergleich verschiedener Messungen wichtig
ist. Dies ist durch die geometrische Interpretation der Farbvalenzen
als Vektoren besonders anschaulich.
Seien R', G', B' die neuen Primärvalenzen, die durch die alten
ausdrückbar sind
R' = a11R + a12G + a13B (21)
und entsprechend für G' und B'.
Wenn wieder je eine trichromatische Einheit der neuen Primärvalenzen für die additive Mischung zu Weiß benötigt werden soll (was im allgemeinen der Fall ist), dann muß man zunächst dafür sorgen und die Intensität der drei Vektoren anpassen:
1/3 (c1R' + c2G' + c3B') = U (22)
wobei für U die gewünschte Unbuntart, E oder ein anderer Weißpunkt, einzusetzen ist.
Dies ist ein System von drei Gleichungen für die drei Unbekannten c1, c2 und c3, das aufzulösen ist. Dann kann man die gewünschten Primärvalenzen neu definieren:
R' : = c1R',
G' : = c2G',
B' : = c3B',
(23)
was auf Neufestlegung der Koeffizienten a11 ... a33 hinausläuft.
Nachdem dies erledigt ist, kann man die Gleichungen (21) nach den "Unbekannten"
R, G, B auflösen.
(Weder die
alten noch die neuen Basisvektoren dürfen in einer Ebene Iiegen.) Man
erhält die Lösung des Gleichungssystens in der Form
R = b11R' + b21G' + b31B'
… (24)
Somit kann man eine Farbe Q auf zwei Arten darstellen
Q = RR +GG + BB = R'R' + G'G' + G'G'
= R (b11R' + b21G' + b31B')
+ G (b12R' + b22G' + b32B')(25)
+ B (b13R' + b23G' + b33B')
Daraus kann man ablesen, wie die Koordinaten umzurechnen sind:
R' = b11R + b12G + b13B
G' = b21R +b22G + b23B (26)
B' = b31R + b32G + b33B
Für Spektralfarben gelten natürlich die gleichen Transformationsformeln, also erhalten wir
‾r'
λ = b11‾rλ + b12‾gλ + b13‾bλ (27)
etc. für die neuen Spektralwertkurven.
Die Transformation für die Farbwertanteile r = R/(R+G+
B) etc.
soll hier nicht angegeben werden, sie ist nicht schwer herzuleiten.
Der Normalbeobachter
Da die drei Kurven ‾rλ, ‾gλ, ‾bλ die Berechnung der Farbvalenz für
jeden Farbreiz gestatten, enthalten sie die gesamte Information über
die Farbwahrmehmung des Beobachters (Farbwahrnehmung im Sinn
von Unterscheidungsfähigkeit, von Empfindungen soll zunächst nicht die Rede sein). Bei noch so sorgfältiger Messung werden allerdings die
entsprechenden Kurven zweier verschiedener Versuchspersonen kaum
je völlig übereinstimmen, sondern es ergeben sich mehr oder weniger
deutliche Unterschiede. Selbst für ein und dieselbe Person hängen die
Ergebnisse von der Größe (Winkelausdehnung) des Testfeldes ab.
Diese für Standardisierung und eindeutige Festlegung von Toleranzen ungünstige Situation wurde 1931 von der Internationalen Beleuchtungskommission (CIE, Commission Internationale de l'Eclairage) behoben, indem ein fiktiver Normalbeobachter (oder Normbeobachter)
eingeführt wurde: Als Grundlage dienten Messungen von Guild (1931/32) und von Wright (1928/29), die mit Farbreizen der schon erwähnten Wellenlängen von λR = 700 nm, λG = 546,1 nm, λB = 435,8 nm
bei einem Öffnungswinkei von 2° gewonnen worden waren, und deren
Mittelwerte dann als Spektralwertkurven für den Normalbeobachter
definiert wurden. Die Kurven sind in Abb. 6 dargestellt. Spätere Wiederholungen der Messungen mit verfeinerter Messtechnik (Stiles 1955)
haben die früheren Ergebnisse bestätigt, die Kurven können also als
repräsentativ gelten.
Die einfache Umrechnungsmöglichkeit zwischen Primärvalenzen hat
die Internationale Beleuchtungskommission 1931 bewogen, für die Erfassung und graphische Darstellung von Daten Primärvalenzen mit
besonderen Eigenschaften anzugeben und die entsprechenden Spektralwertfunktionen in Tabellenform als Norm festzulegen. Die neuen
Primärvalenzen X, Y, Z wurden so gewählt, dass die Maßzahlen X,
Y, Z für reelle Farben nicht negativ werden, d. h. in der Einheitsebene liegt der Spektralfarbenzug innerhalb des Dreiecks XYZ, und das
bedeutet natürlich auch, dass die Valenzen X, Y, Z selbst nicht realisierbar sind, sie liefern nur das Koordinatensystem für eine besonders
bequeme Darstellung.
Gl. (14) gibt die Helligkeit für jeden Vektor im Farbraum an. Setzen
wir L = 0, dann ist
0 = lR R + lG G + lB B (28)
die Gleichung einer Ebene im Farbraum, der Ort aller Valenzen mit
Helligkeit Null. Die Primärvalenzen X und Z wurden in diese Ebene
gelegt, daher gilt lX = lZ = 0. Für die Valenz Y wurde als Spektralwertkurve die Helligkeitsempfindungskurve Vλ angenommen, denn
unter der Voraussetzung, dass Helligkeiten additiv sind, kann man diese Kurve als Überlagerung der Spektralwertkurven ‾rλ, ‾gλ, ‾bλ ausrechnen, entsprechend Gl. (14). Somit wird die Koordinate Y proportional
zur Helligkeit.
Da die Form des Farbdreiecks – wie schon besprochen – willkürlich
ist, wählt man üblicherweise die bequemste Form, nämlich ein rechtwinklig gleichschenkliges Dreieck, Abb. 9, die den Vorteil hat, dass man
normales Millimeterpapier verwenden kann.
Um dieses Dreieck nicht allzu farblos erscheinen zu lassen, sind
in Abb. 10 die Farben, wie sie ein Computer-Monitor mit Kathodenstrahlröhre zeigen kann, dargestellt. (Genaueres dazu finden Sie im nächsten Abschnitt über Farbwiedergabe.)
Die Berechnung der Farbmaßzahlen in bezug auf X, Y, Z geschieht völlig analog zu den Gleichungen (17) mit Hilfe der Spektralwertkurven ‾xλ, ‾yλ und ‾zλ, Abb. 11: Aus der spektralen LeistungsVerteilungsfunktion (Farbreizfunktion) berechnet man die trichromatischen Maßzahlen entsprechend
X = k∑λ‾xλφλΔλ,
Y = k∑λ‾yλφλΔλ,
Z =k∑λ‾zλφλΔλ. (29)
Da die Funktionen ‾xλ, ‾yλ, ‾zλ willkürlich normiert sind (so dass das
Maximum von ‾yλ gleich 1 ist), haben wir hier einen Proportionalitätsfaktor vor die Summe gestellt.
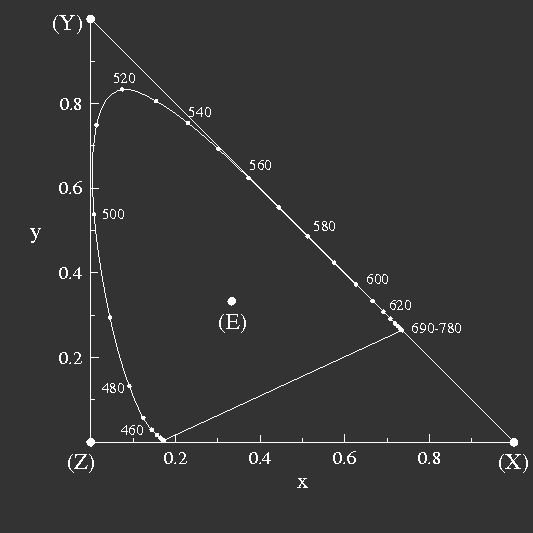
Bild 9: Die Normfarbtafel, aufbauend auf den virtuellen Farbvalenzen
X,
Y und
Z. Entlang des Spektralfarbenzuges sind die Wellenlängen
in nm angegeben.
Bei der Wellenlänge λ = 555 nm entspricht einem Energiestrom
von 1 W (Watt) ein Lichtstrom von 683 lm (Lumen). Diese Zahl berechnet man aus der Definition der Einheit des Lichtstromes mit Hilfe
der Schwarzkörperstrahlung und der Planckschen Formel. Wählt man
also k = Km = 683 lm/W, so gibt Y den Gesamtlichtstrom in Lumen
an, wenn für φλ der Energiefluss pro Wellenlängeneinheit eingesetzt
wird.
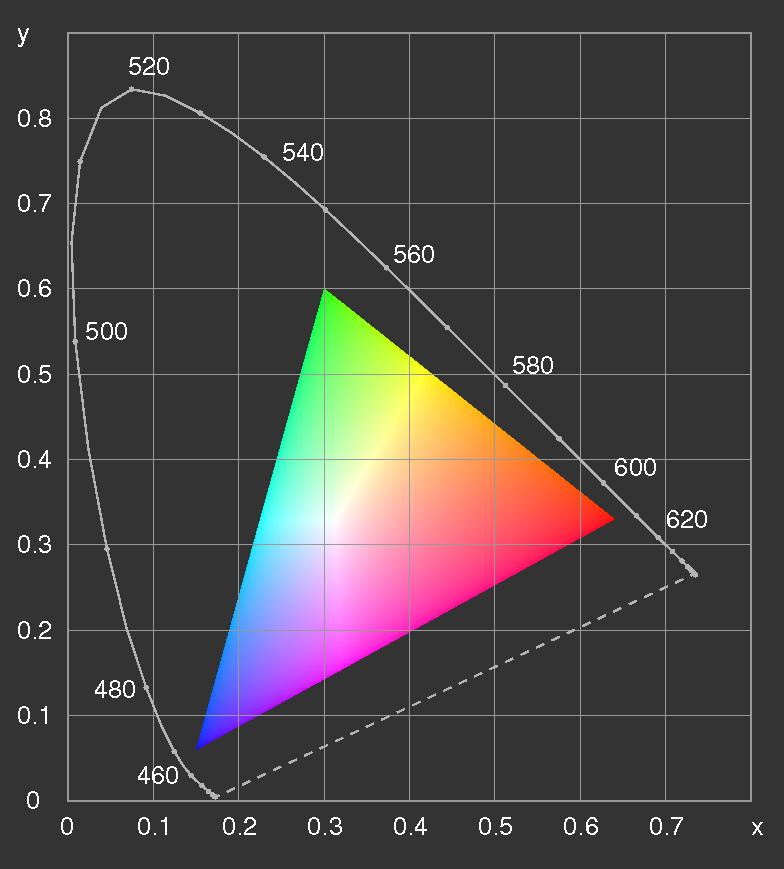
Bild 10: Die Normfarbtafel mit den durch drei Primärvalenzen, wie
sie für Kathodenstrahl-Bildröhren Verwendung finden, darstellbaren
Farben. Die Farben sind jeweils in maximaler Helligkeit eingetragen.
Als "Weiß" ist D65 festgelegt. (Solange nicht
sichergestellt ist, dass die Leuchtsubstanzen genau den angenommenen Farbvalenzen entsprechen und der Monitor auf D65 als Weiß justiert ist, gilt dieses Bild allerdings nur qualitativ.)
Die Farbwertanteile ergeben sich zu
x = X / (X + Y + Z),
y = Y / (X + Y + Z),
z = 1 − x − y. (30)
Die Beziehung für die Helligkeit L = lxX + lyY + lxZ wird wegen
lx = lz = 0, ly = 1 zu
L = Y . (31)
Die eben besprochenen Spektralwertkurven wurden für 2° Gesichtsfeldöffnungswinkel bestimmt und sind bis etwa 4° Öffnungswinkel gültig
(2° Öffnungswinkel entspricht einer Scheibe von 1 cm Durchmesser aus 29 cm Entfernung betrachtet). Für die Fälle, wo es auf die Beurteilung
größerer Gesichtsfelder ankommt, wurden 1964, basierend auf Messungen von Speranskaya (1959) und Stiles (1955), Kurven und Valenzen
für 10° Öffnungswinkel festgelegt, die zur Unterscheidung von den anderen mit dem Index 10 versehen werden, also X10, … ‾x10,λ, X10 etc.
Allerdings ist Übereinstimmung von Y10 mit der Helligkeit zunächst
nicht vorauszusetzen, da eine entsprechende Helligkeitsempfindungskurve noch nicht festgelegt ist (DIN 5031 und DIN 5033).
Körperfarben und Farbfilter
Bei dem bisher über Farbmessung gesagten sind wir immer von der
Farbreizfunktion φλ ausgegangen, also von der spektralen Zusammensetzung des Lichts, das in die Pupille eintritt. Falls φλ direkt durch die
Emission einer Lampe oder sonstigen Lichtquelle bestimmt ist, oder
durch eine als Einheit aufgefasste Kombination Lampe-Filter, dann ist
alles im vorigen Abschnitt gesagte unmittelbar anwendbar. Nun begegnen wir aber Farben überwiegend an farbigen Gegenständen, und
dementsprechend bezieht sich die Farbmessung in den meisten Fällen
auf Farben von Oberflächen (Aufsichts-, Oberflächen- oder Körperfarben), oder von Filtern, wobei die Farbreizfunktion außer durch
Remissions- (bzw. Transmissions-) Vermögen des Körpers durch die
Beleuchtungsart wesentlich mitbestimmt wird. Da man die Einflüsse
beider auf die Farbe nicht trennen kann, muss man die Beleuchtungsart
festlegen, um verschiedene Messungen vergleichen zu können. Von der
CIE wurden drei Standardlichtquellen A, B, C vorgeschlagen, die so
gewählt sind, dass sie
"Glühlampenlicht",
"Sonnenlicht am Mittag",
und
"Tageslicht bei bedecktem Himmel" nahekommen. Verteilungsfunktionen für weitere Lichtarten wurden genormt: D55, D65 und D75.
Der Buchstabe D steht für daylight, Tageslicht. D65 entspricht mittlerem Tageslicht der Farbtemperatur 6504 K. Die Lichtquelle A wird
realisiert durch eine 500 W Wolframfadenlampe, die bei einer Farbtemperatur von 2856 K betrieben wird; B und C sind A mit Filtern.
Die optischen Eigenschaften einer Körperoberfläche, soweit sie für
die Farbigkeit relevant sind, werden durch den Remissionsfaktor
(Remissionsgrad oder kurz Remission) beschrieben. Dieser gibt an,
wieviel Licht von einer Fläche im Verhältnis zu einer ideal mattweißen
unter den gleichen Bedingungen zum Beobachter gelangt, und zwar
als Funktion dar Wellenlänge:
βλ = L/Lweiß (32)
bei Beleuchtung mit Licht der Wellenlänge λ.
Für eine ideal mattweiße Fläche, die nicht absorbiert und unter
allen Beobachtungswinkeln gleich hell erscheint, ist definitionsgemäß
βλ = 1. (33)
Was im folgenden über Aufsichtsfarben gesagt wird, gilt auch für
Farbfilter, wobei nur das Remissionsvermögen βλ durch das Transmissionsvermögen τλ (Transmission, Durchlässigkeit) zu ersetzen ist.
Für eine anschaulich-qualitative Beurteilung des Remissionsvermögens βλ, etwa von Farbpapier, reicht schon ein Prisma: Man legt einen
schmalen Streifen des Papiers auf einen schwarzen Untergrund und
daneben zum Vergleich einen Streifen aus weißem Papier, die man
beide durch das Prisma anschaut. Im Vergleich mit dem Spektrum des
vom weißen Streifen reflektierten Lichts sieht man gut, welche Anteile
vom Farbpapier nur wenig zurückgeworfen werden.
Die beleuchtende Lichtart sei durch die spektrale Verteilungsfunktion Sλ gegeben, wobei SλΔλ dem Energiefluss von der Lichtquelle im
Bereich der Wellenlängen von λ−Δλ/2 bis λ+Δλ/2 proportional ist.
Da der Absolutwert für unsere Zwecke nicht interessiert, wird Sλ meist
willkürlich normiert (d. h. die Kurve wird mit einem Faktor multipliziert, so dass sie an einer bestimmten Stelle den Wert 1 annimmt).
Trifft der Energiestrom SλΔλ auf die betrachtete Fläche auf, so ist
der zum Beobachter reflektierte Energiestrom proportional zu SλΔλ
und zum Remissionskoeffzienten βλ, also
φλΔλ = βλ⋅SλΔλ (34)
für alle Wellenlängen. Daraus kann man die Farbmaßzahlen berechnen
X = k∑λ‾xλβλSλΔλ,
Y = k∑λ‾yλβλSλΔλ,
Z = k∑λ‾zλβλSλΔλ. (35)
wobei die Konstante k üblicherweise so gewählt wird, dass sich für eine
ideal mattweiße Fläche die Maßzahl Y, die die Helligkeit angibt, zu 1
oder 100% ergibt
k = 100 [∑λ‾yλ⋅SλΔλ]−1. (36)
Y gibt also die relative Helligkeit gegenüber einer vollkommen weißen
Fläche in Prozent an, den sogenannten Hellbezugswert, und dadurch
hat man für die Maßzahl der Helligkeit Unabhängigkeit von der Beleuchtungsstärke erreicht. Dies ist für Körper- oder Aufsichtsfarben
äußerst wichtig: Denn in Gegensatz zu farbigem Licht, wo Helligkeit
und Farbart als getrennte Eigenschaften wahrgenommen werden, trägt
bei Oberflächenfarben die Helligkeit (im Vergleich zu Weiß) wesentlich zur Farbempfindung bei. Während es kein braunes Licht gibt,
allenfalls orangefarbenes geringer Helligkeit, wird eine Oberfläche mit
den gleichen Farbmaßzahlen wie Orange, aber geringerer Helligkeit Y ,
nicht als dunkelorange, sondern als braun gesehen.
Farben (Valenzen) mit den gleichen Koordinaten x, y, aber abgestufter Helligkeit Y nennt man eine Schattenreihe.
dass die Farbart von Braun und Orange gleich sind, oder die von
Gelb und Olivgrün, kann man experimentell mit Hilfe von zwei Projektoren schön veranschaulichen: Zunächst projiziert man in einem
abgedunkelten Raum Licht durch ein oranges oder gelbes Filter mit
nicht zu großer Helligkeit auf eine Leinwand; die Farbempfindung ist
Orange bzw. Gelb. Dann wird mit größerer Helligkeit ein weißer Ring
auf die Leinwand projiziert, und sofort erscheint das Innere des Ringes
braun bzw. oliv.
Bei der Bewertung von Körperfarben ist durch die allgemeine Beleuchtung schon ein Vergleichsstandard vorhanden, so dass die Empfindung Braun auch ohne weiße Vergleichsfläche zustande kommt.
Bei Körperfarben erhält der Ausdruck
"bedingt gleich" oder
"metamere Übereinstimmung" zweier Farbvalenzen besondere Bedeutung,
da die Farben (Farbvalenzen) von der Beleuchtung mitbestimmt werden, wie jeder weiß und wie in den Formeln zum Ausdruck kommt.
Wenn wir für zwei verschiedene Oberflächen Farbgleichheit feststellen,
dann gilt dies zunächst nur für die eine Beleuchtungsart, bei anderer
Beleuchtung kann die Übereinstimmung verloren gehen. Der Unterschied, der dabei auftreten kann, ist natürlich umso größer, je verschiedener die Remissionskurven voneinander sind, so dass es sinnvoll
ist, von starker oder schwacher Metamerie zu sprechen.


Bild 12a, b: Metamere Übereinstimmung von Farben kann beim Wechsel der Beleuchtung verlorengehen. Die Bilder zeigen eine Demonstration am
Universum® Bremen. (Die Bilder können durch Anklicken vergrößert werden.)
Bei sehr "ungewöhnlichen" Remissionskurven kann die Abhängigkeit der Farbe von der Beleuchtung überraschend stark sein. Ein berühmtes Beispiel ist der Edelstein Alexandrit, der bei Kerzenlicht rot, bei Tageslicht aber blau erscheint.
Farbkörper, Farbatlanten
Bei Körperfarben ist, wie eben besprochen, die relative Helligkeit (gegenüber Weiß), und nicht die absolute Helligkeit, die von der Beleuchtung abhängt, für die Farbempfindung maßgeblich. Daher bilden die
Körperfarben, im Gegensatz zu den Valenzen farbiger Lichter, die im
Farbraum innerhalb einer nach oben offenen Farbtüte liegen, einen
allseits begrenzten Farbkörper, Bild 13. Dabei liegen die Valenzen der
sattesten im täglichen Leben auftretenden Farben etwas innerhalb der Oberfläche des Farbkörpers, die von den sogenannten Optimalfarben gebildet wird. Optimalfarben sind die Farben, die bei gegebener
Farbart (x, y, z) die größte theoretisch mögliche Helligkeit Y haben,
bei gegebener Helligkeit die größte Sättigung. Man kann zeigen, dass
das Remissionsvermögen von Optimalfarben nur die Werte Null oder
Eins haben darf, mit höchstens zwei Sprungstellen.

Bild 13: Innerhalb der von den spektralen Valenzen im Farbraum aufgespannten "Tüte" liegt der Farbkörper der möglichen Oberflächenfarben. Als Beleuchtung ist "Tageslicht" D65 vorausgesetzt, daher entspricht der höchste Punkt des
Körpers (mit
Y = 1) dieser Beleuchtung. Der Körper ist durch Querschnitte gleicher Valenz-Einheitenzahl dargestellt.
Farbmustersammlungen
Es hat verschiedene Versuche gegeben, Farbkörper für Aufsichtsfarben zu entwerfen und Farbmusterkarten für Farbbewertungszwecke
herauszugeben, wobei angestrebt wurde, dass die Abstände den Empfindungsunterschieden entsprechen. Es sollen hier nur drei Beispiele
erwähnt werden, der Ostwaldsche Farbkörper, das Munsellsche System
und die DIN Farbenkarte. Die frühen Entwürfe von Farbkörpern, die
nur noch von historischem Interesse sind, wurden in den Vorlesungen
nur kurz abgehandelt; mehr findet man im "Museum".
Wilhelm Ostwald (1923) klassifiziert die Farben nach dem Anteil an maximal gesättigter Farbe ("Vollfarbe", optimale Farbe), dem
Weiß- und Schwarzanteil, und die Maßzahlen F, W, S sind genau die,
die man bei Mischung mit dem Farbkreisel, der noch besprochen wird,
den Segmentgrößen entnehmen kann. Es ist F + S + W = 1.
Der Farbkörper des amerikanischen Malers A.H. Munsell (Munsell
1915 und später) basiert auf der Ordnung der Farbvalenzen nach Farbton (hue), Helligkeit (value) und Sättigung oder Farbintensität (chroma), wobei die Abstufung in erster Linie nach subjektiven Gesichtspunkten (gestützt auf Farbkreiselmessungen) erfolgte. In diesem Farbsystem kommt die größere Helligkeit von Gelb im Vergleich zu Blau
in den value-Maßzahlen zur Geltung. Bemerkenswert ist, dass die Linien konstanten Farbtones, in die Farbtafel eingetragen, gekrümmt sind:
die als farbtongleich empfundenen Farbmuster zunehmender
"Verweißlichung" entsprechen im allgemeinen nicht einer festen
"farbtongleichen" Wellenlänge, oder umgekehrt: Bei der Mischung (optisch oder
mit Pigmentfarben) einer Farbe mit Weiß empfindet man eine Farbtonverschiebung ("Abney-Effekt"), desgleichen auch bei
"Verschwärzlichung" ("Bezold{Brücke{Effekt"). Tatsächlich lagen die ursprünglichen Farbmuster auf etwas welligen Linien, Farbmessungen dienten
später dazu, die Linien durch Neuauswahl der Muster zu glätten. Bild
14 zeigt den Aufbau zweier Seiten aus dem
"Munsell Book of Color".
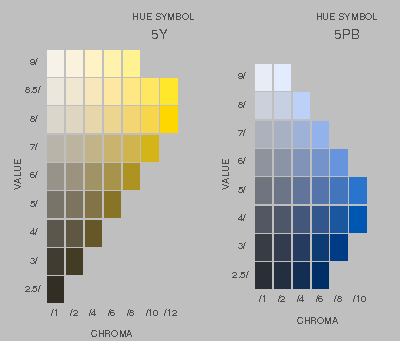 |
| Bild 14: Schematische Wiedergabe zweier Seiten aus dem Munsell Book of Color, die die Anordnung der Farbmuster zeigen. (Die stellenweise sichtbaren Abweichungen im
Farbton sind durch die begrenzte Zahl möglicher Farbabstufungen auf dem Computer bedingt, wo für jede Grundfarbe nur 256 verschiedene Intensitäten möglich
sind.)
|
Die DIN Farbkarte schließlich stellt ein Ordnungssystem dar, das
auf empirisch gefundenen und daher komplizierten Formeln für Helligkeit und Sättigung aufbaut, um gleichabständig wirkende Sättigungs- und Schattenreihen zu gewinnen.
Die Farbmerkmale nach DIN 6164 sind folgende: Farbton T: Läuft
von 1 bis 24. Die empfindungsmäßige Tonänderung beim Fortschreiten
auf einer Geraden in der Farbtafel wurde im Interesse einer einfachen
Umrechnung hingenommen.
Sättigungsstufe S: am besten einer graphischen Darstellung (DINFarbtafel) zu entnehmen.
Dunkelstufe D: ein Maß für die Helligkeit bezogen auf die Optimalfarbe gleicher Farbart (D = 0 für idealesWeiß und alle Optimalfarben,
D = 10 für Schwarz).
Eine Farbe wird gekennzeichnet durch die Angabe von T, S und D,
wobei die Maßzahlen durch Doppelpunkte getrennt werden, z. B. Farbe
7:3:2 DIN 6164. Zu erwähnen ist noch, dass nicht versucht wurde, die
Schrittweiten von einer Sättigungsstufe zur nächsten für verschiedene
Dunkelstufen einander anzugleichen. Man zog vor, das Diagramm für
alle Dunkelstufen festzuhalten, was wieder der bequemen Umrechnung
in trichromatische Maßzahlen X, Y, Z zugute kommt. (Richter 1950,
1955 a,b)
CIE-xyY-Farbkörper
Statt im Farbvalenzraum (Bild 13) kann man den Farbkörper bequemer im Raum der Koordinaten x, y, Y aufbauen (Rösch 1928, Mac
Adam 1935). Für die beide Varianten des Farbkörpers gilt aber, dass
die Abstände mit den empfindungsmäßigen Unterschieden nicht übereinstimmen, siehe Bild 10, das man auch als Aufsicht auf den durch
die drei Primärvalenzen darstellbaren Teil des CIE-xyY-Farbkörpers
deuten kann, und Bild 15, das als horizontaler Schnitt bei konstanter
Helligkeit Y zu deuten ist.
Farbabstände, CIE-L*u'v', CIE-L*u*v*, …
Die Farbkoordinaten x, y, die wir eingeführt haben, enthalten in der
Wahl der Primärvalenzen eine gewisse Willkür. Diese Willkür hat aber
nur geringen Einfluss auf die graphische Darstellung, eine andere Wahl
der Primärvalenzen führt auf eine
"perspektivische Verzerrung" der
Farbtafel, zusammen mit einer Neufestlegung der Einheiten derart,
dass die bequeme Berechnung der additiven Farbmischung (Hebel- oder
Schwerpunktsgesetz) erhalten bleibt.
Unter einem Gesichtspunkt ist die Normfarbtafel recht unbefriedigend: die Abstände der Farbarten in der Tafel entsprechen nicht den
subjektiv empfundenen Farbunterschieden.
Dies ist weiter nicht erstaunlich, da wir ja bis jetzt die Empfindung,
sofern sie über das Gleichheitsurteil hinausgeht, völlig ausgeklammert
haben. Wenn eine Empfindung, z. B. die der Farbabstände, in die Untersuchung mit einbezogen wird, so geht das über unsere anfängliche
Beschränkung hinaus.
Man kann ein Maß für den empfindungsgemäßen Abstand aus
der Unterscheidbarkeit benachbarter Farbvalenzen gewinnen, die sich
z. B. in der Streuung der Messpunkte bei oft wiederholtem Farbvergleich äußert. Solche Untersuchungen wurden von Mac Adam (1942)
durchgeführt. Andere Ansätze stammen von Schrödinger und von Stiles (1946).
Man kann eine andere Schnittebene als die Einheitsebene zur Darstellung der Farbarten verwenden, in der die Abstände in der Farbtafel annähernd den empfundenen Farbunterschieden entsprechen. So
kam das 1960 CIE-UCS Diagramm (UCS: Uniform chromaticity scale),
auch 1960 CIE u,v-Diagramm genannt, zustande. Die neuen Koordinaten berechnet man aus x und y wie folgt:
u =
4x/(−2x + 12y + 3), v = 6y/(−2x + 12y + 3), (37)
und umgekehrt
x = 3u/(2u − 8v + 4), y = 2v/(2u − 8v + 4). (38)
Der Übergang in das UCS-Diagramm ist eine Transformation von
der gleichen Art wie der früher besprochene Wechsel von einem Satz
Primärvalenzen zum anderen. Dieses System wurde abgelöst durch das
1976 CIE-L*,u',v' Diagramm. (L* steht für die Helligkeit, auf die wir
später genauer eingehen wollen.)
u' = 4x/(−2x + 12y + 3), v' = 9y/(−2x + 12y + 3). (39)
Empfindungsmäßig gleichabständige Farbkörper, bei denen also
gleiche Abstände gleichen empfundenen Farbunterschieden entsprechen, sind streng genommen unmöglich. Aber Farbkörper, die diesem
Ideal nahekommen, näher als CIE-XYZ (Bild 13) oder CIE-xyY jedenfalls, gibt es glücklicherweise doch.
 |  |
|
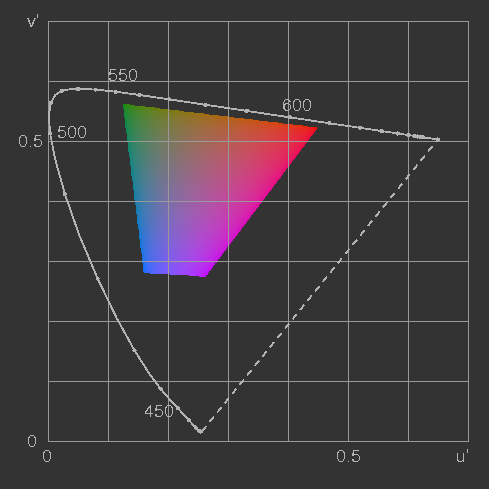
Bild 15: Die annähernd gleichabständige CIE u'v' Normfarbtafel.
Man vergleiche mit dem nächsten Bild! |
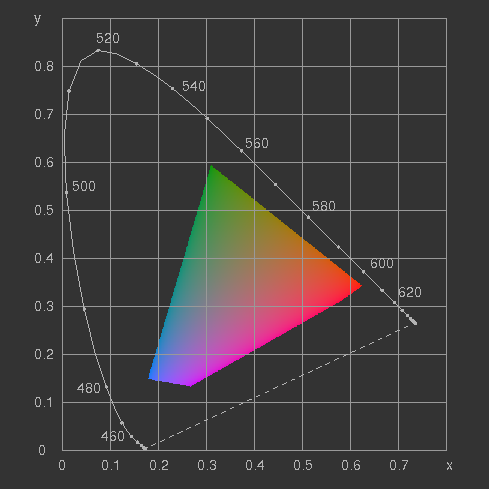
Bild 16: Die Normfarbtafel wie Bild 10 mit gleicher Helligkeit. |
Die in Bild 15 gezeigte Auftragungsweise erfüllt bei festgehaltener
Helligkeit die Forderung schon recht gut. Sollen aber auch die Helligkeitsunterschiede als gleichmäßig gestuft empfunden werden, dann
darf als Maß für die Helligkeit nicht Y verwendet werden, denn bei zunehmender Helligkeit erscheinen gleiche Schritte von Y immer kleiner.
Das Weber-Fechnersches Gesetz beschreibt diesen Sachverhalt, gilt
aber auch nicht streng, da darin die Adaptation auf die Umgebungshelligkeit unberücksichtigt bleibt. Geringe Umgebungs-Helligkeit voraussetzend (wie beim Fernsehen üblich) wurde in einem Vorschlag der
CIE von 1976 der Zusammenhang zwischen Y und der empfundenen
Helligkeit L* durch ein Potenzgesetz angenähert,
L* = 1.16(Y/Yn)1/3 − 0.16 für Y/Yn > 0.008856
L* = 9.033 Y/Yn sonst,(40)
und aus den oben eingeführten Koordinaten u', v' die neuen Koordinaten u*, v* gemäß
u* = 13L*(u' − u'n),
v* = 13L*(v' − v'n)
berechnet, wobei Yn; u'n, v'n die entsprechenden Koordinaten des Weiß-Bezugspunktes (beim Bildschirm) oder der Lichtquelle sind.
In den so eingeführten 1976 CIE-L*u*v*-Koordinaten kommt der
Farbkörper der empfindungsmäßigen Gleichabständigkeit sehr nahe.
(Es ist üblich, Y in Prozent anzugeben, dadurch werden dann die
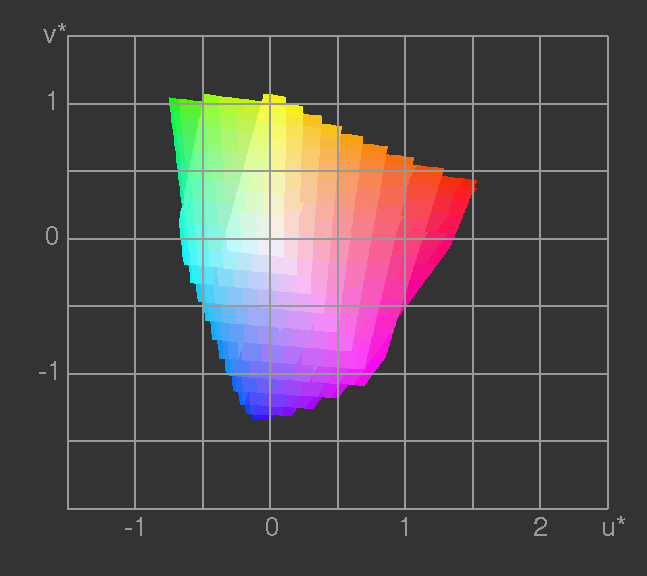
Maßzahlen L*, u* und v* hundertmal so groß.) Die Bilder 17 und 18
zeigen den darstellbaren Teil des Farbkörpers in zwei Ansichten jeweils
als Stapel von Schichtflächen gleicher Helligkeit.
 |  |
|
Bild 17: Durch die drei Primärvalenzen einer Kathodenstrahlröhre
darstellbaren Farben im CIE-L*u*v*-Diagramm
|
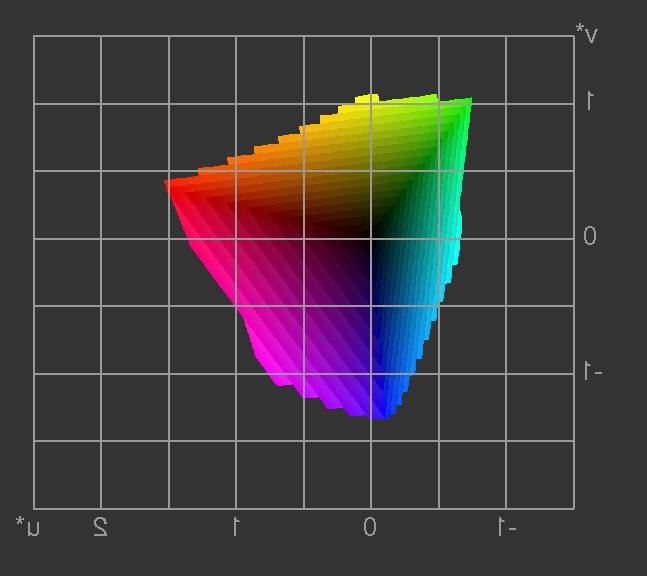
Bild 18: Das vorige Bild, sozusagen von hinten gesehen (dunkle Seite
des Farbkörpers im CIE-L*u*v*-Raum)
|
Eine weitere Parametrisierung des Farbraumes mit etwas einfacheren Umrechnungsformeln wurde im gleichen Jahr vorgeschlagen, 1976
CIE L*a*b* genannt.
Auf der Helligkeitsachse wird L* aufgetragen, in den beiden anderen dazu senkrechten Richtungen die Koordinaten a* ("Rot minus
Grün") und b* ("Gelb minus Blau"), die wie folgt berechnet werden:
a* = 5[f(X/Xn) − f(Y/Yn)]
b* = 2[f(Y/Yn) − f(Z/Zn)],
wobei
f(t) = t1/3 für t > 0.008856
f(t) = 7.787t + 16/116 sonst
(41)
und Xn, Yn, Zn die Maßzahlen vom Referenz-Weiß sind.
Die Rücktransformation lautet (für Y/Yn > 0.008856) bei Normierung von L*max = 1
P = (L* + 0.16)/1.16,
X = Xn(P + a*/5)3,
Y = YnP3,
Z = Zn(P − b*/2)3.
Es ist zu betonen, dass die Vektoraddition zur Berechnung der additiven Farbmischung nur im CIE-XYZ-Raum möglich ist. Aufgrund
der nichtlinearen Transformationsformeln gibt es im L*u'v'-, L*u*v*und L*a*b*-Raum keine so einfachen Zusammenhänge.
Wegen der annähernd erreichten empfindungsmäßigen Gleichabständigkeit des CIE L*a*b* Farbraumes kann man den Abstand
Δ12 = [(L*1 − L*2)2 + (a*1 − a*2)2 + (b*1 − b*2)2]1/2 (42)
als Maß für Farbtoleranzen verwenden.
Zurück zur Übersicht „Farben sehen, messen und wiedergeben"
Weiter: Farbwiedergabe
Legal Information Data Privacy