
Through the amount of photos we see today, we have become so accustomed to the perspective two-dimensional representation of three-dimensional scenes that we hardly ever realize that our sense of sight gives us no perspective images. We see our surroundings three-dimensionally. Of course: with increasing distance, the angular size of any object decreases.

This fact may be called perspective, and with a bit of geometry that's all there is to it. There are no mysterious and incomprehensible effects.
A perspective representation of a scenery on a flat surface is designed to give the impression of spatial depth. A woodcut by Albrecht Dürer shows how this can be mastered by drawing:

Note the sharpened stick placed in front of the draughtsman's eye as an aid to always bring the eye to the same position. The angles seen on the resulting drawing are only exactly the same as the original ones if you look at them from exactly the same distance as the eye had from the plane with the crossed threads. For photographs, the correct distance for viewing is the focal length of the lens multiplied by the magnification factor. This condition is usually not fulfilled, but our sense of sight is quite tolerant here.
Many modern cameras offer the possibility of panorama shots. During recording, you rotate around your axis moderately fast and get a 360° panorama as a result. Let's examine the following situation: someone stands on a small island in the middle of the ocean and sees the horizon all around. He takes a 360° panorama and still ordinary photos – on all pictures, the horizon appears as a straight line. This is of course due to the fact that the earth is so big and the water surface is therefore only so slightly curved that we cannot perceive it.
But what would it look like if the earth were much smaller? Not as small as the Little Prince's dwarf planet, but with a radius Rfictitious = 6371 m, that's about one thousandth of the Earth's radius. (The simple formulas you need to calculate the distance of the horizon etc. are given at elsewhere.) The photographer keeps the camera exactly horizontal at 10 m above sea level while taking a panoramic picture and an ordinary photo. The results would then be like this:


The horizon appears 3.21° below eye level and is completely straight in the panorama image. This must be the case, because when the photographer rotates, he always sees the horizon at the same height. The panorama, sufficiently enlarged and bent into a cylinder shell, would have to be viewed from the center to appear “lifelike”.
In the usual wide-angle shot on the right, however, the horizon is slightly curved. The light rays that go from the horizon to the eye form a cone. The line of intersection of this cone with the image surface is a hyperbola, the vertex of which we see in the image. So this is the perspective projection of the horizon onto a flat surface, in this example the flat sensor of the camera.
The retina of our eyes is not flat, and we also always turn our eyes or head in the direction we are looking. Therefore, what we see is more like a panoramic image than a simple photograph, which means that even with an earth reduced to a thousandth of its size, we would hardly notice the curvature!
To see a similar amount of the earth's curvature, one would have to photograph the earth from an altitude of ten kilometres. I don't have a suitable photo, but I found a video on Youtube, which shows pictures from an airplane with an infrared filter from this height, on which the horizon can be seen.


In the bizarrely entertaining video entitled “Maximum Destruction of the Globe Theory”, Google Earth and Global Positioning System (smartphone with GPS) are used to try to prove that the Earth is not a globe. The argument is the visibility in the infrared, which is much greater than it is calculated under the assumption of straight light rays. The fact that the light rays in the atmosphere are slightly curved due to the refraction was not considered. (The curvature of the rays depends on the weather conditions.)
But on the video footage you can actually see the curvature of the horizon! The horizon here is the border between the light landmass and the slightly darker band above, the lower atmosphere. The cloud layers at different heights above also show the curvature. In the screenshot here it becomes even clearer if you squeeze the picture horizontally. You can see the result on the right in comparison to the calculated image compressed likewise.
I was not able to determine how large the focal length of the zoom lens was in this section of the film, but it should roughly correspond to the one used for the above calculation, as can be seen from the curvature. The calculations made for the photo simulations are also valid for this case, one only needs to replace meters by kilometers and therefore gets the same pictures.
Whether the proponents of Flat Earth themselves believe what they upload to the net is difficult to judge in individual cases. It started with Samuel Birley Rowbotham in the 19th century and his writing “Earth Not a Globe”. His alleged evidence of flatness can be found today on the Internet without criticism and repeated many times. Rowbotham's texts and simple schematic sketches have only been replaced by YouTube videos with animated graphics.
Rowbotham goes to great lengths to explain intricately, lengthily and completely wrongly how what he calls the Law of Perspective works. He may have outwitted himself, or he may have trusted that those he is targeting will not follow his long explanations and simply believe the wrong result.
And I guess that's how it happened. Apparently none of the Flat-Earth believers has really thought about what perspective is and how it works. According to Rowbotham, the sun orbits at a constant altitude above the flat and stationary earth, sunrise and sunset arise “from the operation of a simple and everywhere visible law of perspective.” This is illustrated by the following drawing:
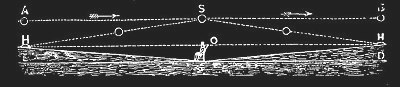
“In the diagram, fig. 64, let the line E, D, represent the surface of the earth; H, H, the morning and evening horizon; and A, S, B, a portion of the true path of the sun. An observer at O, looking to the east, will first see the sun in the morning, not at A, its true position, but in its apparent position, H, just emerging from the “vanishing point,” or the morning horizon. At nine o'clock, the sun will have the apparent position, 1, gradually appearing to ascend the line H, 1, S; the point S, being the meridian or noonday position. … ”
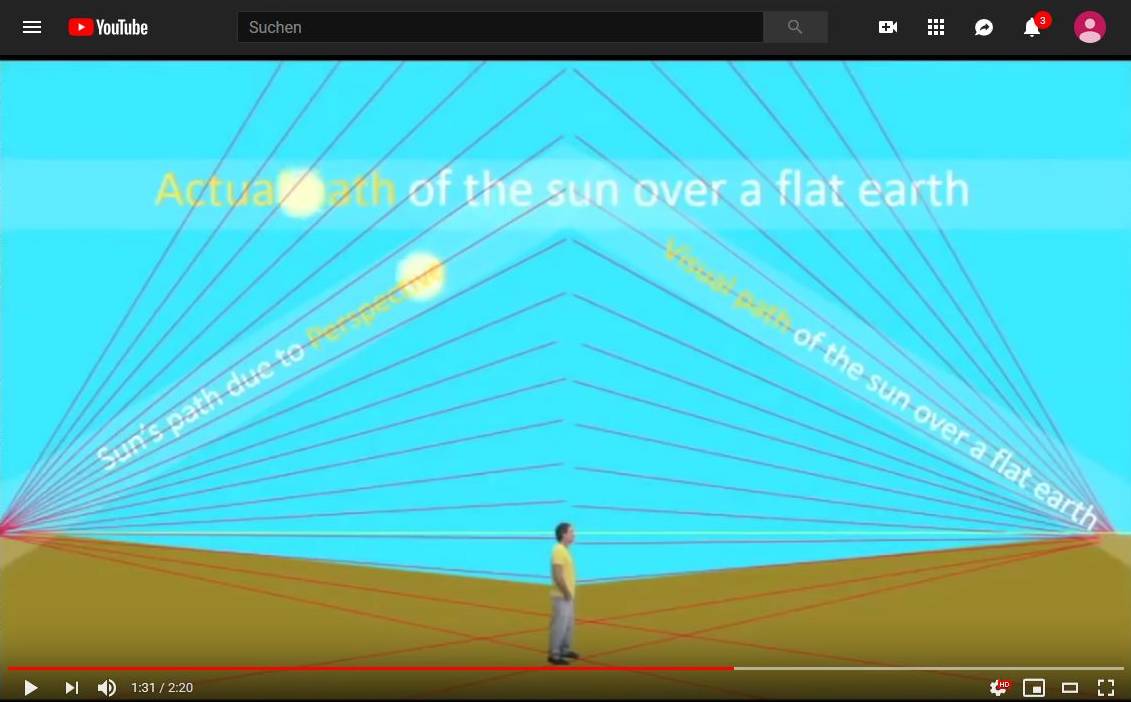
For comparison a screenshot from a video “Law of Perspective”, which does without any explanatory text – it would be interesting to learn why in this case the object seen (the sun) is always seen the same size, why it reaches the vanishing point even though it is supposedly not far away, and, and …
Today's flat-earth apologists claim that the sun orbits at an altitude of about 5000 km above the earth's disk. The result of a simple calculation: in Rome at the winter solstice at midnight the sun should then be visible 15° above the horizon in the north.
Legal Information Data Privacy