


Queteletsche Ringe sind vielleicht nicht allzu selten; ich habe diese Erscheinung aber bis jetzt nur gesehen, wenn ich sie absichtlich erzeugt habe. Man findet im Netz sehr schöne Beispiele, wo solche Ringe durch Staub oder Algen auf der stillen Oberfläche einer Pfütze oder eines Tümpels entstehen. [1], [2],[3], [4].
Vor kurzem hat Aleksandr Berdnikov drei Fotos von einem eingestaubten Spiegel hochgeladen, die dieses Phänomen sehr deutlich zeigen:
Die Bilder (Quelle: Wikimedia Commons [A], [B], [C]) wurden mit verschiedenen Abständen von Kamera und Lampe vom Spiegel aufgenommen: das Licht näher am Spiegel (ungefähr halb so weit wie die Kamera, erstes Bild), doppelt so weit entfernt wie die Kamera (mittleres Bild) und schließlich Kamera und Leuchte ungefähr gleich weit vom Spiegel (rechtes Bild).
Aleksandr Berdnikov hat die relativen Positionen von Lampe und Kamera in den Kommentaren zu den Bildern beschrieben, aber das kann auch aus den Bildern selbst entnommen werden, wenn die relativen Entfernungen bekannt sind.
Im rechten Bild sind Spiegelbild von Kamera und Lichtquelle zu sehen, man sieht die Anordnung also. Auf den anderen beiden Bildern ist die Kamera nicht zu sehen – die dunkle Fläche in der rechten unteren Ecke vom Bild links muss jedoch die Rückseite des Lampengehäuses sein, es ist also rechts von der Kamera und etwas tiefer. Im zweiten Bild wiederum kann die dunkle Fläche in der rechten unteren Ecke nur vom Schatten der Kamera herrühren (im Schatten und darunter spiegelt sich die Umgebung), das Licht ist also links hinter der Kamera und höher als diese. (Die Bilder lassen sich durch Draufklicken vergrößern.)
Die Ringe sind kreisförmig, aber anders als bei Ringen um Sonne oder Mond sieht man hier nicht die Lichtquelle im Mittelpunkt.
Zunächst betrachten wir den im Freien zu beobachtenden Fall von Ringen, die von Algen wie Chromulina rosanoffii (oder Staubpartikeln) auf der ruhigen Oberfläche einer Pfütze oder eines Teiches hervorgerufen werden. Wie von Marko Riikonen [4] gezeigt wurde, erheben sich diese eigenartigen Algen auf dünnen Stielchen über die Wasseroberfläche.
Die Farben entstehen durch die Interferenz des Lichtes, das auf zwei verschiedenen Wegen zum Auge gelangt: erst Reflexion an der Wasseroberfläche, dann Streuung am Teilchen darüber oder erst Streuung am Teilchen und dann Reflexion. Die beiden Lichtwage sind auf der nebenstrehenden Schemaskizze als schwarze und weiße Linie eingezeichnet.
Der Effekt tritt allerdings nur auf, wenn das streuende Teilchen und sein Spiegelbild nicht mehr getrennt wahrgenommen werden können, so dass sich die Wellen am gleichen Punkt auf der Netzhaut des Auges (oder des Sensors der Kamera) überlagern. In der Skizze rechts müsste das Auge daher ein paar tausendmal weiter weg sein, wenn sie maßstabsgetreu sein sollte.
Wenn man weiß, dass die Ringe konzentrische Kreise sind (das werde ich noch zeigen), dann ist es einfach, deren Mittelpunkt zu bestimmen. Auf dem hellsten Kreis sieht man das Spiegelbild der Sonne, dort sind beide Wege gleich lang und daher gibt es keine Auslöschung. Ein zweiter, leicht zu findender Punkt, wo die beiden Lichtwege gleich lang wären, ist der Gegenpunkt zur Sonne im Schatten des Beobachters. Der Kreismittelpunkt liegt genau in der Mitte zwischen beiden, also genau in der Richtung zum Erdmittelpunkt.
Das ist nicht mehr so, wenn die Lichtquelle näher ist. Statt des Gegenpunktes zur Sonne ist genau der Punkt zu wählen, der durch die Lampe verdeckt wird (B im nebenstehenden Bild), oder der Punkt, wo sich der Schatten des Auges (des Objektivs der Kamera) befände (B in der Skizze ganz rechts). An einem staubigen Spiegel kann man die Ringe nur sehen, wenn die (von der Senkrechten auf den Spiegel aus gemessenen) Beleuchtungs- und Beobachtungswinkel sehr klein sind. Die beiden Graphiken rechts zeigen nicht nur, wie man den Mittelpunkt findet, sondern auch, dass sich das Bild nicht ändert, wenn die Positionen von Auge und Kamera vertauscht werden.
Für die drei Fotos unten wurde ein runder Spiegel mit 11 cm Durchmesser verwendet. Beim linken und mittleren Bild war die Glühlampe ungefähr 5 m, die Kamera 2.5 m vom Spiegel entfernt, diese Bilder unterscheiden sich nur in der Entfernungseinstellung: die Ringe werden deutlicher, wenn nicht auf den Spiegel, sondern auf das Spiegelbild der Lampe scharf gestellt wird.
Beim dritten Bild in der Reihe war die Kamera ebenfalls in 2.5 m Abstand, das Lampenlicht wurde so durch eine Glasscheibe auf den Spiegel gelenkt, dass der „Punkt B“ nicht durch das Lampengehäuse verdeckt wurde; die effektive Entfernung betrug nur ca. 80 cm.



Um zu zeigen, dass die bunten Ringe kreisförmig sind, betrachte ich zunächst diesen einfacheren Fall wo das Licht von der Sonne kommt. Die Koordinaten werden so gewählt, dass die z-Achse nach oben zeigt, die x-Achse nach links und die y-Achse nach vorne aus dem Bildschirm heraus. Der Koordinatenursprung befinde sich auf der Höhe der Wasseroberfläche genau unter dem Auge. Die verwendeten Größen und Bezeichnungen sind der nebenstehenden Skizze zu entnehmen; das streuende Teilchen befinde sich im Abstand d über dem Wasser.
Bis zum Erreichen der gelben Linie in der Skizze haben der schwarz gezeichnete und der weiße Lichtstrahl gleich lange Wege zurückgelegt. Das Wegstück des schwarzen Strahls von der gelben Linie zur Wasseroberfläche und von dort zum streuenden Körnchen wird s1 genannt. Der Weg des weißen Lichtstrahls vom streuenden Teilchen über die Wasserfläche und bis zum Auge ist so lang, als ob er vom Spiegelbild des Teilchens käme. So ergibt sich der Unterschied der Weglängen zu Δ = s1−s2.
Es ist s1=2d cos(θ) und s2=2d cos(α). Damit wird
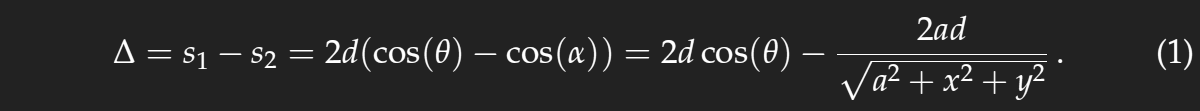
Der Weglängenunterschied bestimmt die Farbe, die man sieht. Für ein festes Δ erhält man nach kurzer Rechnung die Gleichung eines Kreises
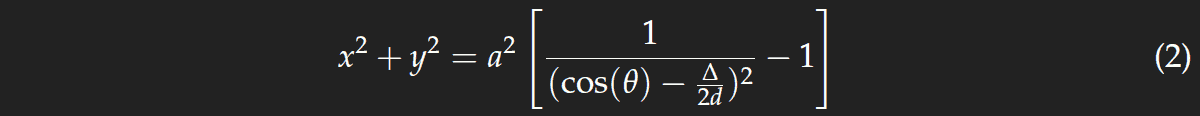
mit dem Mittelpunkt im Ursprung.
Jetzt betrachten wir eine Lichtquelle im Abstand von nur wenigen Metern und einen angestaubten Spiegel statt der Wasseroberfläche. Das Spiegelglas, auf dem die Staubpartikeln liegen, habe die Dicke d, der Abstand der Teilchen von der silbrigen Rückseite ist daher groß im Vergleich zu den Wellenlängen des Lichts und daher sind die Ringe nur zu sehen, wenn die Winkel α und β sehr klein sind. Beim Eintritt in das Glas wird das Licht gebrochen, die entsprechenden Winkel α' und β' sind durch das Snellsche Brechungsgesetz bestimmt. Da die Winkel sehr klein sind, kann man sin(α) durch α ersetzen etc. und erhält
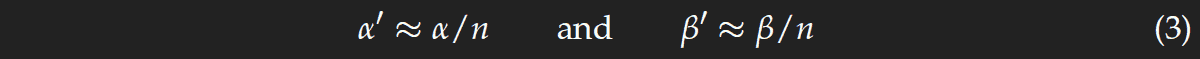
wobei n der Brechungsindex des Glases ist. Die beiden Skizzen rechts zeigen, dass
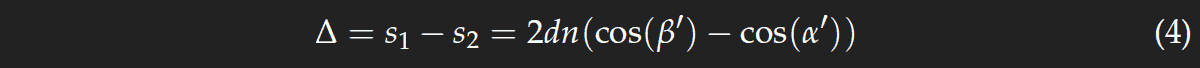
Hier taucht der zusätzliche Faktor n auf, da nicht der geometrische, sondern der optische Wegunterschied maßgeblich ist. Unter Benutzung von Gl. (3) und cos2(x)=1−sin2(x), erhalten wir
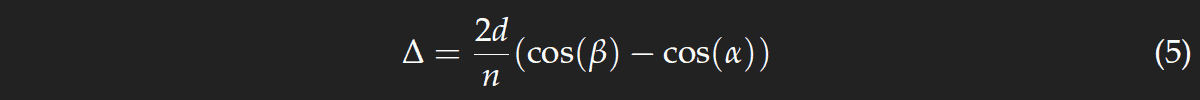
und daraus
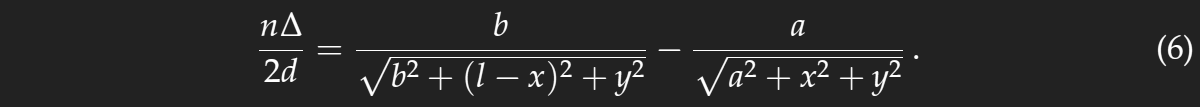
Die Abstände a und b sind viel größer als die Entfernung l und die Beträge der Koordinaten x und y, die hier von Interesse sind. Das ermöglicht weitere Näherungen. Man kann Ausdrücke wie (1+x)−1/2 durch 1−x/2 annähern, wenn |x|<<1. Damit erhalten wir einen Kreis
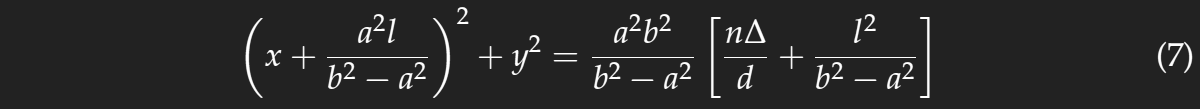
dessen Mittelpunkt weder das Spiegelbild der Lampe noch das des Auges ist. Die Lage des Mittelpunktes hängt nicht von Δ ab, die Ringe sind daher konzentrische Kreise.

Zurück zur Übersicht