Wasser
Die html-Formatierung und benutzerdefinierte Anweisungen wurden auf diesem Server deaktiviert. Die gleiche Datei mit angepasster Formatierung finden Sie hier: https://farbeinf.de/static_html/wasser.html.
Reines Wasser ist kristallklar, farblos – aber an klaren, tiefen Gewässern sehen wir, dass es doch schwach bläulich-grünlich ist. Beim Blick aufs Meer oder einen See mischt sich diese Farbe des Wassers mit der des reflektierten Himmels und des Untergrundes. Schwebstoffe können darüberhinaus die Eigenfarbe des Wassers überdecken.

Die Ostsee.

Gletscherbach im Yoho National Park, British Columbia, Canada. Die Trübung durch Schwebstoffe läßt die Eigenfarbe des Wassers deutlich werden. Die Schwebstoffe selbst (Gesteinsmehl) würden wir im trockenen Zustand als weißes oder hellgraues Pulver sehen. (Die Teilchen sind klein, aber doch zu groß, um durch den
Tyndall-Effekt Farbe hervorzurufen.)
Foto © Henrik Zawischa
 
| Ein weißer Eimer, links voll Wasser, rechts leer. Die Höhe des Wassers betrug 25 cm; die Aufnahmen entstanden bei bedecktem Himmel.
|
In einem aufwendigeren Experiment sieht man die Farbe deutlicher: Blick durch ein vier Meter langes, weites, mit reinem Wasser gefülltes Rohr aus Acrylglas gegen eine weiße Fläche, fotografiert im Universum® Bremen. Der experimentelle Aufbau ist
hier zu sehen.
|
 |
Woher rührt diese blaugrüne Farbe?
Elektronen können in den Wassermolekülen durch sichtbares Licht nicht in angeregte Zustände befördert werden – dazu reicht die Energie der Photonen nicht. Erst durch Ultraviolettstrahlung sind elektronische Anregungen möglich. Aber es gibt noch andere Molekülanregungen: Schwingungen und Rotationen. Um Rotationen anzuregen reichen winzige Energien. Die Frequenzen der Vibrationen sind ebenfalls viel niedriger als die des sichtbaren Lichtes: das Absorptionsmaximum für Wärmestrahlung infolge der Anregung von Schwingungen liegt bei Wellenlängen zwischen 2500 und 3000 nm, also weit im Infraroten.
Trotzdem sind die Vibrationen die Ursache der Farbe des Wassers. Den experimentellen Beweis dafür lieferten
C.L. Braun und S.N. Smirnov (J. Chem. Edu., 1993, 70(8), 612) durch den Vergleich der Absorptionsspektren von Wasser (H2O) und schwerem Wasser (D2O).
Das soll im folgenden erläutert werden.
|
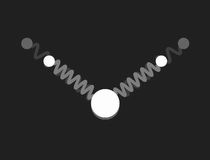
Im freien Wassermolekül – H2O – schließen die Bindungen der Wasserstoffkerne an den Sauerstoff einen Winkel von ca. 104.5º ein. Dies hat ein großes Dipolmoment zur Folge (die Wasserstoffatome tragen positive Überschussladung, der Sauerstoff negative). Das nebenstehende Bild zeigt ein mechanisches Modell zur Veranschaulichung der Geometrie: die Bindungen sind durch masselose Federn symbolisiert, die in Ruhelage den genannten Winkel einschließen.
|
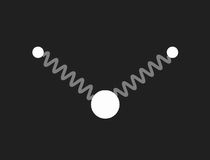 |
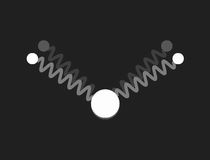
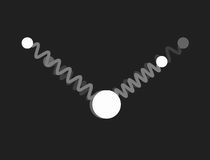
Beschränkt man sich bei der Untersuchung des mechanischen Modells auf kleine Schwingungen, so findet man drei Formen einfach periodischer (harmonischer) Schwingungen (Eigenschwingungen, Moden), und die zugehörigen Frequenzen. Diese werden durch die folgenden Bilder veranschaulicht:
Die drei Eigenschwingungen des Wassermoleküls im mechanischen Modell: links die symmetrische Streckschwingung, in der Mitte die Biegeschwingung und rechts die unsymmetrische Streckschwingung. Doppelklicken auf die Bilder startet die Animation, einfaches Klicken schaltet sie wieder aus. Ein Klick auf das Zeichen ◊ unter einem Bild startet die Animation in einem neuen Fenster.
Für Wasserdampf wurden die Frequenzen der drei Schwingungsformen ermittelt (siehe z.B.
Herzberg, G. Infrared and Raman Spectra; D. Van Nostrand: Princeton, 1945; p. 281); sie entsprechen den Absorptionsmaxima, diese liegen bei den Wellenlängen 2.74 μm, 7.27 μm, 2.66 μm, weit außerhalb des sichtbaren Bereichs, der ungefähr von 0.4 μm bis 0.7 μm reicht.
Harmonische und anharmonische Schwingungen
Unter harmonischen Schwingungen versteht man reine Sinusschwingungen; sie ergeben sich, wenn die rücktreibende Kraft genau proportional zur Auslenkung ist. Dies ist in den meisten Fällen eine Idealisierung, doch der harmonische Oszillator stellt eines der wichtigsten Modelle in der Physik überhaupt dar.
Um die Diskussion einfach zu halten, betrachten wir die Schwingung eines Massenpunktes in einem fest vorgegebenen Kraftfeld. Die Bewegung soll nur in einer Richtung möglich sein, wir wählen diese als x-Richtung.
Die rücktreibende Kraft sei proportional zur Auslenkung, dann schwingt der Oszillator
unabhängig von der Amplitude immer mit der gleichen Frequenz. In graphischer Darstellung hat das Potential der Kraft die Form einer Parabel.
Die quantenmechanische Behandlung des harmonischen Oszillators soll hier nicht skizziert werden. Wichtig ist der Sachverhalt, dass Energie nur in Quanten hν aufgenommen und abgegeben werden kann, wobei h das Plancksche Wirkungsquantum und ν die Frequenz der Schwingung ist. Daraus ergibt sich für die möglichen Energien eine gleichabständige "Leiter". Dipolübergänge können nur zwischen benachbarten Energieniveaus stattfinden.
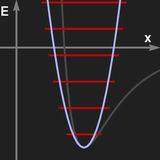
Links: Das Potential einer harmonischen Schwingung und die sich ergebenden Energieniveaus.
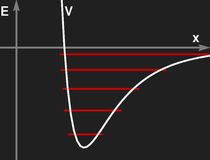
Rechts: Die Form eines realistischen effektiven Potentials für Molekülschwingungen, qualitativ. Die Energieniveaus, die sich in einem solchen Potential ergeben, sind nicht mehr gleichabständig.
Die beiden Graphiken oben zeigen einen Vergleich zwischen einem realistischen Potential zwischen Molekülbausteinen (rechts) und einem (in Ruhelage und Krümmung) an dieses angepassten Oszillatorpotential.
Für das realistische Potential ist schon die klassische Behandlung der Schwingung nicht ganz einfach. Am einfachsten ist heute die numerische Integration der Bewegungsgleichung mithilfe des Computers.

Zwei Schwingungen in dem oben rechts skizzierten Potential mit verschiedener Amplitude.
Bei kleiner Amplitude erscheint die Schwingung noch annähernd harmonisch (= sinusförmig), bei größerer Amplitude werden die Abweichungen von der Sinusform deutlich. Die weiß gezeichnete Kurve lässt sich als Summe aus einer konstanten Auslenkung, einer sinusförmigen Grundschwingung und einer Oberschwingung mit der doppelten Grundfrequenz annähern. (Ähnliches ist in der Akustik wohlbekannt: die Obertöne machen den Klangcharakter von Musikinstrumenten aus.)
Ein Oszillator kann auch durch Einwirkung einer periodischen Kraft mit der Frequenz der Oberschwingungen in Resonanz versetzt werden. Dieser Sachverhalt hat eine quantenmechanische Entsprechung: im harmonischen Oszillator sind nur Übergänge zwischen benachbarten Niveaus "erlaubt", in anharmonischen Oszillatoren sind auch Dipolübergänge zwischen weiter voneinander entfernten Energieniveaus möglich.
Entsprechendes findet man beim Wassermolekül. Die Grundfrequenzen liegen weit im Infraroten, aber mit geringer Wahrscheinlichkeit können auch Übergänge stattfinden, die den Oberschwingungen entsprechen, also von Grundzustand gleich in höher angeregte Vibrationszustände führen. So kommt es zu einer ganz geringen Absorption im langwelligen, roten Bereich des sichtbaren Lichtes.

Emerald Lake, Yoho National Park, British Columbia, Canada.
Foto © Henrik Zawischa
Wasser und Eis
Die Wechselwirkung der Moleküle im Wasser führt zu einer geringen Verschiebung der Absorptionsmaxima und zu einer Verbreiterung der Absorptionslinien, aus denen breite Buckel werden. Entsprechendes geschieht in der geordneten Anordnung der Moleküle im Eis:
die Kräfte (Wasserstoffbrücken), die die Moleküle an ihren Plätzen und in ihrer Orientierung halten, haben zur Folge, dass sich Schwingungen wellenartig über den ganzen Kristall ausbreiten. Diese Wellen unterliegen natürlich auch der Quantenmechanik, die entsprechenden Energiequanten hν nennt man Phononen. Für die Gitterschwingungen ergeben sich Frequenzbänder, ganz analog, wie es bei der Behandlung der
Festkörper erläutert wurde. Die Lage der Bänder ist in erster Linie durch die Frequenzen der freien Moleküle bestimmt. Es gibt daher keinen großen Unterschied in der Farbe von flüssigen Wasser und Eis.
Schweres Wasser
Schweres Wasser zeigt nicht die blaugrüne Farbe. Das Absorptionsspektrum ist dem von normalem Wasser sehr ähnlich, nur zu niedrigeren Frequenzen verschoben (siehe Braun & Smirnov). Dadurch erreichen auch die höchsten merklichen Absorptionen den sichtbaren Bereich nicht mehr.
Andere Substanzen
Es ist gut möglich, dass andere Substanzen, die uns farblos erscheinen, aus dem gleichen Grund genau so schwach bläulich wären wie Wasser, wenn sie in genügend großen Massen zu sehen wären. Wasser ist in der Menge seines Vorkommens einzigartig.
Zurück zur Übersicht: Wie kommt Farbe zustande?