Wellenschleppen von Enten und Schiffen

Die Wellen, die Enten erzeugen, wenn sie geradeaus schwimmen, zeigen eine verblüffende Ähnsichkeit mit denen von Booten oder Schiffen. William Thomson (Lord Kelvin) hat schon 1887 gezeigt, dass der Winkel, den das V-förmige Wellenmuster an der Spitze bildet, immer derselbe ist, unabhängig davon, ob die Wellen von einem Schiff oder einer Ente hervorgerufen werden, solange das Wasser tief genug ist (tiefer als die Wellenlänge der erzeugten Wellen) [1].

Die mathematische Behandlung von Wasserwellen ist kompliziert, (siehe z.B. den Wikipedia-Artikel), aber manche Ergebnisse kann man doch ganz leicht mit elementarer Mathematik erreichen [2].

Während sich Schallwellen unabhängig von der Tonhöhe oder Wellenlänge mit der gleichen Geschwindigkeit ausbreiten, hängt die Geschwindigkeit von Wasserwellen von der Wellenlänge ab, und zwar sind im tiefen Wasser lange Wellen schneller als kürzere. (Wir betrachten hier nur die sogenannten Schwerewellen.) Dies kann man durch eine einfache Dimensionsbetrachtung herausfinden.

Wovon kann die Ausbreitungsgeschwindigkeit der Wasserwellen abhängen? Von der Wellenlänge λ, klar, von der Wassertiefe H, von der Erdbeschleunigung g, von der Dichte des Wassers ρ, von der Oberflächenspannung σ und wovon vielleicht noch?

Die Oberflächenspannung wirkt sich nur bei sehr kurzen Wellenlängen (im Millimeterbereich) aus, die können wir hier vernachlässigen. Wenn das Wasser tief ist, sozusagen unendlich tief, dann kann auch die Wassertiefe in dem Ausdruck für die Geschwindigkeit nicht vorkommen.

Wenn wir eine Gleichung der Form

haben, dann muss dieses “irgendetwas” die Dimension einer Geschwindigkeit haben, also Länge geteilt durch Zeit. Die Wurzel aus Wellenlänge mal Erdbeschleunigung hat diese Dimension, daher können wir schließen, dass die Geschwindigkeit proportional zu dieser Wurzel ist, also:

(Der exakte Ausdruck für die Phasengeschwindigkeit ist v_φ = √gλ ⁄ (2π) .)

Die Phasengeschwindigkeit ist, grob gesprochen, die Geschwindigkeit der einzelnen Wellenkämme. Ein Wellenzug endlicher Länge bewegt sich aber mit der Gruppengeschwindigkeit vorwärts, und die ist in diesem Fall nur halb so groß. (Dies folgt aus dem allgemeinen Ausdruck für die Gruppengeschwindigkeit, siehe z.B. diesen Wikipedia-Artikel.) Wenn wir in einem Wellenzug einen bestimmten Wellenkamm verfolgen, sehen wir, dass er sich schneller bewegt als das ganze Bündel. Wenn er sich der Vorderfront nähert, wird er schwächer und verschwindet schließlich. Aber hinten entsteht ein neuer Kamm, wird stärker, und dann wieder schwächer, wenn er sich der Vorderfront nähert …

Die Gruppengeschwindigkeit ist halb so groß wie die Phasengeschwindigkeit, das ist alles, was man braucht, um das Wellenmuster in groben Zügen zu verstehen.

	Betrachten wir zunächst den fiktiven Fall, dass alle Wellen die gleiche Geschwindigkeit haben, 80 % der Bootsgeschwindigkeit, Phasen- und Gruppengeschwindigkeit übereinstimmen. Die resultierende Welle finden wir mit Hilfe des Huygensschen Prinzips (Bild links). Das Boot erregt kontinuierlich Wellenimpulse; die Kreise sind die Elementarwellen, die von den markierten Punkten ausgegangen sind. Die resultierende Stoßwelle ergibt sich als Einhüllende, dort kommen alle Elementarwellen gleichzeitig an und bauen sich zur Stoßwelle auf, während sie sich an allen anderen Stellen nicht verstärken.
	Als nächstes nehmen wir an, dass das Boot richtige Wasserwellen erzeugt, betrachten aber nur eine ganz bestimmte Wellenlänge und Frequenz. Die von den markierten Punkten ausgegangenen Elementarwellen sind nicht so weit vorangekommen, dass sie sich zur Stoßwelle überlagern hätten können, sondern haben nur den halben Weg bis zu den roten Punkten zurückgelegt, ergeben also eine schmälere Wellenschleppe und keine Stoßwelle.
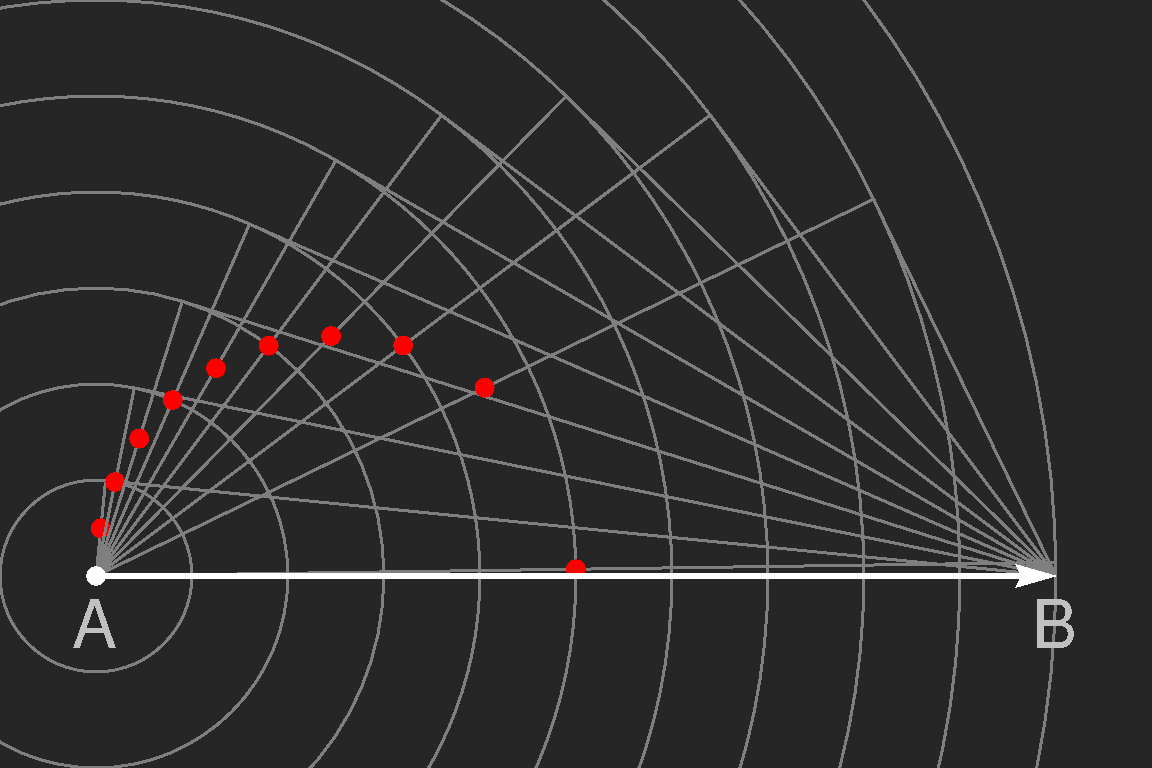
	Das Boot erzeugt an jedem Punkt seiner Bahn ein Wellenpaket, das sich als Überlagerung von vielen verschieden langen Wellen darstellen lässt. In der nebenstehenden Skizze ist die Konstruktion des Ausbreitungswinkels für die Phasengeschwindigkeiten von 10, 20, 30 … 99.99 Prozent der Bootsgeschwindigkeit eingezeichnet. Die roten Punkte markieren die Stellen, wo die vom Punkt A ausgegangenen Wellen ankommen, wenn das Boot im Punkt B ist. Aus der Konstruktion ist ersichtlich, dass die roten Punkte auf einem Kreisbogen liegen, dessen Radius ein Viertel der Strecke AB ist. Man beachte, dass der Ausbreitungswinkel der Wellen, deren Phasengeschwindigkeit mit der Geschwindigkeit des Bootes übereinstimmt, 0° beträgt, sie also dem Boot folgen.
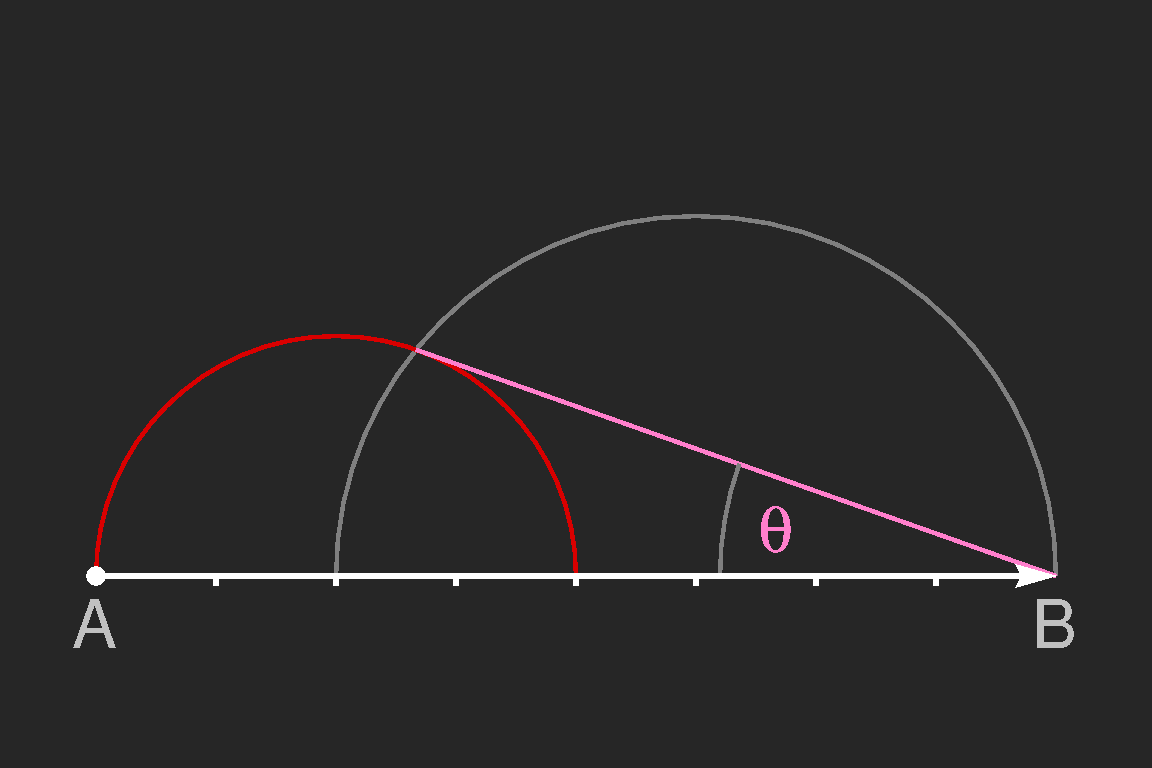
	Jetzt kann man leicht den maximalen Ausbreitungswinkel θ aller möglichen Wellen bestimmen. Der Rand der Wellenschleppe ist durch die vom Punkt B aus gezogene Tangente an den roten Kreis bestimmt. Da sich die benachbarten Wellenlängen unter nahezu dem gleichen Winkel ausbreiten, sind dort die Wellen am stärksten ausgeprägt. An der Skizze sieht man, dass sin(θ) = 1/3, und somit θ = 19.47°. Diese Beziehung hat William Thomson gefunden, und sie gilt, solange die Gruppengeschwindigkeit gleich der halben Phasengeschwindigkeit ist.
	Wellen, deren Geschwindigkeit gleich der des Bootes (oder der Ente) ist oder ihr nahekommen, folgen dem Boot (oder der Ente) unter kleinerem Winkel und bilden die Schleppe von transversalen Wellen. Das gesamte Wellenmuster scheint starr mit dem Boot verbunden, wenn dieses mit konstanter Geschwindigkeit geradeaus fährt.

Stark motorisierte schnelle Boote erzeugen scheinbar schmälere Schleppen. Dies wurde vor einiger Zeit von Rabaud und Moisy [3] untersucht, siehe auch [4], [5]. Es rührt daher, dass Wellen, deren Länge größer ist als der Bootsrumpf, nur mit umso geringerer Amplitude angeregt werden, je länger sie sind.

Impressum    Datenschutz