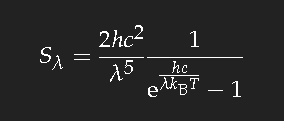The html formatting and custom instructions have been disabled on this server. The same file with adapted formatting can be found here: https://farbeinf.de/static_html/blackbody.html.
Line spectra are due to the discreteness of atomic and molecular energy levels – how can continuous spectra be emitted at all, as the sun and other thermal radiators are composed of atoms too?
Let us consider first glowing gas, like the sun. The high temperature indicates that the constituent particles are moving with high average energy, frequently colliding and following paths of very irregular shapes (in a semiclassical description). Atoms get ionized, free electrons also move erratically. All the electrically charged particles on their curved and jagged paths are surrounded by an electric field which has to follow the erratic motion and therefore changes rapidly. Because of the coupling between electric and magnetic fields, the local changes of the electric field propagate in space as waves with quite irregular time dependence. It is, however, possible to decompose the irregular shape and time dependence into a sum or integral of harmonic waves of different frequencies – a continuous spectrum of frequencies (or wavelengths) results. (In the correct quantum mechanical treatment, trajectories are abandoned. Instead, one deals with transitions between unbound states of electrons which themselves form a continuum.)
The situation is similar in a glowing solid or liquid. Instead of the single atoms or ions, in this case one has to consider the whole bulk system, as the particles are in permanent interaction with their neighbours. Thermal motion of electrons and ions is again irregular enough so that the above arguments are applicable.
Flames shine if they contain particles of soot glowing and burning. This can be seen in the example of a candle's flame:
|
In the lowest part of the flame there are no particles of soot, as there is abundant oxygen and the combustion of the vaporized wax is complete. There a weak bluish light can be seen which is emitted in the chemical reaction of combustion. Higher up in the flame there is less oxygen, and the remnants of partially burnt wax molecules agglutinate, forming soot particles emitting orange-coloured light in the heat of the flame. |
 |


Left: Candle flame mirrored in a black glass plate.
Its colour can better be judged from the weaker mirror image, since the flame itself is over-exposed.
Right:
Choosing the shutter speed such that the flame is not over-exposed, the surroundings are not seen any more. The colour of the flame is the same as that of its mirror image in the left picture.
(For these pictures, the white balance has been set to "Cloudy", see below. Settings: ISO 100, f:5.0. Left: 1/60 sec. Right: 1/1600 sec.)
Comparison with the next figure allows to estimate that the temperature in the brightest parts of the flame is almost 2000 Kelvin.
Glow
It is remarkable how little the intensity and its distribution over the different wavelengths depend on the glowing substance. Radiation emerging from a small opening in a cavity depends only on the temperature and not at all on the material of the cavity's walls. The opening of a cavity appears black at low temperatures and represents an almost ideal black body; the radiation emitted is called black-body radiation or cavity radiation. Given the temperature, the black-body radiation is completely specified. Light of the sun is similar to blackbody radiation.

Colours of blackbody radiation as a function of temperature, starting at 1000 K. The distance between ticks is 1000 K.
From thermodynamical considerations it follows that the emissivity of any material is proportional to its absorptivity, which means that at high temperature a body shines the brighter, the darker it is when cold. If the absorptivity of a body is the same for all visible wavelengths, it appears grey. When heated, it does not shine as bright as a black body, but the relative intensity distribution and thus the colour is the same. The filaments of incandescent bulbs are made of tungsten, a grey metal. Knowing its temperature one knows also the spectral distribution of the emitted light.
Without derivation Planck's radiation law is quoted, which marked the beginning of modern physics:
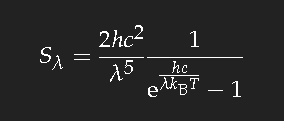 Here SλΔλ is the amount of energy radiated per unit time and unit area into a unit of solid angle perpendicular to the surface; h is Planck's and kB Boltzmann's
constant; T is the temperature measured in Kelvin, c is the velocity of light.
Here SλΔλ is the amount of energy radiated per unit time and unit area into a unit of solid angle perpendicular to the surface; h is Planck's and kB Boltzmann's
constant; T is the temperature measured in Kelvin, c is the velocity of light.
Only thermodynamical statistics and the fact that electromagnetic waves are quantized in units of energy hν (where ν is the frequency ν = c/λ) are used to obtain this formula.
Blackbody radiation is of fundamental importance for lighting technology and science of measuring: The luminous density of the black body at the temperature of solidifying platinum is by definition 600 000 cd/m2
(candela per square meter), this allows to obtain photometric quantities from energetic ones. Due to advances in metrology, this original definition has been replaced in 1979 by the CGPM. New definition:
The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540·1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian.
The kind of illumination, important for photography and film, is specified by colour temperature.
Colour temperature
As already mentioned, the spectral composition of sunlight is similar to that of a black body. The differences are mainly due to the earth's atmosphere which scatters short wavelengths more than longer ones. This makes the sky blue and direct sunlight somewhat yellowish. But even then the radiation ist similar to that of a black body, only with somewhat lower temperature as the sun, whereas the blue of the sky resembles blackbody radiation of much higher temperature.
Depending on daytime and weather the quality of daylight undergoes big changes, but can in most cases be specified by the temperature of an equivalent black radiator. This holds even better for artificial light sources like candles, oil lamps and incandescent bulbs.
Thus it is possible in many cases to characterize the kind of illumination by the temperature of an equivalent black body. This is called colour temperature. Only in the case of black and ideal grey bodies it agrees with the true temperature. (In a candle flame the black particles of soot emit the light.)
As our visual system is optimally adapted to daylight (and its changes), one tries to imitate daylight conditions also with artificial light sources as closely as possible (e.g. with fluorescent lamps), and thus colour temperature can be a valid characterization also for non-temperature radiation.
White balance
The eye adapts so well to the brightness and colour temperature of the illumination that we are likely to underestimate how big the differences are. The importance of this adaptation is clear: the perceived colours of surfaces shall remain constant in spite of changing lighting conditions which allows to easily recognize things.
A white sheet of paper appears white also in the light of an incandescent lamp. And if on a photograph there appears a white sheet of paper, it should again be perceived as white. To achieve that, there are different kinds of photographic film for daylight and artificial light, and, additionally, filters have to be used if necessary. Digital cameras perform the white balance by computing. The colour determined for each pixel of the raw image is transformed such that the colour corresponding to the colour temperature (pre-set or determined automatically) is rendered as a neutral grey or, at maximum lightness, as white.


Candle before a black mirror.
Left: white balance set to "Cloudy" (6500 K),
Right: white balance set to "Tungsten" (3000 K)
Back to the page “the origins of colour”
Legal Information Data Privacy