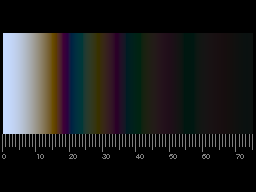
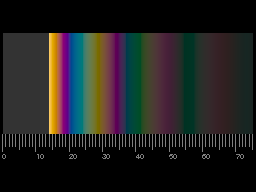Diffraction and Interference
The html formatting and custom instructions have been disabled on this server. The same file with adapted formatting can be found here: https://farbeinf.de/static_html/diffraction.html.
Diffraction phenomena are not really rare, but mostly they gain little attention.



Left: A steel ruler is held before the sun such that the camera's lens is completely shaded. Though there is no straight ray from the sun to the "eye" of the camera, where the ruler hides the sun its edges are shining. Light is diffracted into the shadow region towards the camera. This is a consequence of the wave nature of light; behind an obstacle, waves always expand somewhat into the shadow region.
Middle and right: Without the danger of dazzling glare, this can also be conveniently observed with the moon. It is seen that the length of the bright lines corresponds to the apparent diameter of the moon.
Here we are interested mainly in colours resulting from diffraction and interference, i.e. superposition of diffracted waves.
Light, electromagnetic waves, coherent and incoherent light
Interference phenomena prove the wave nature of light. The following animated picture shows the superposition of waves which have passed narrow slits in an obstacle.
 |
Double-slit experiment:
A plane wave moves towards an absorbing screen with two very narrow slits.
The outgoing waves on the right hand side interfere, constuctive and destructive interference alternating. Double-click on the image will start the animation; a single click will stop it again.
Click
HERE to see the animation in a separate window!
|
Huygens proposed the suggestive idea that any point of a wave front may be considered as the source of daughter waves which superpose each other and thus build up the propagating wave. In the picture above the two openings in the screen are the sources of the secondary waves.
Considering slits wider than the wavelength of the light, things become more difficult. In forward direction, there is constructive interference of the daughter waves originating from different parts of the slit, but at a certain angle, the waves will extinguish each other; while at still larger angles the intensity increases again, then decreases, until the next zero is attained . . . This occurs also if there is only one slit in the diaphragm. On a distant screen, one would see an intensity distribution as shown in the following picture:
 |
Diffraction pattern of a single slit. Upper part: monochromatic light, lower part: white light. As the position of the dark bands depends on the wavelength, white light yields less clear patterns, and colours appear.
|
Now imagine, that in the above simulation of the double-slit experiment, one would replace the incoming plane wave by a mixture of waves coming from slightly different directions, with slightly differing wavelengths and without definite phase relations. The left part of the picture would look like waves in a pool excited by the wind. In the right part of the figure, the waves coming through the two openings still would interfere, however, the mutual enhancement or cancellations would be distributed randomly and would not be stationary, but would change rapidly. Doing the experiment with light, one would not see interference fringes, but only a diffuse spot.
A mixture of waves as just described is called incoherent. In most cases diffraction phenomena are not very conspicuous due to the incoherence of the light from most sources. The small angular extension of the sun already makes many of them imperceptible. (Only recently, lasers provide easily manageable, bright light sources with excellent coherence properties.)
Nevertheless, diffraction phenomena can be seen even in the open air. Colours similar to those appearing in the single slit diffraction pattern or those of circular holes (see below) can be seen in iridescent clouds or aureoles of the sun:

Clouds iridescent in an aureole around the sun. At small angular distance from the sun the dazzlingly bright clouds show nacreous colours. (
More pictures.)
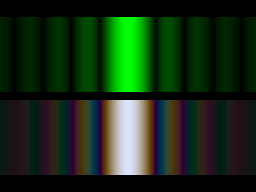
This picture shows the calculated diffraction pattern of a circular hole (see the next images) superimposed on a light grey background. The brightness has been chosen such that at the center (up to 13 units ao the underlying scale) is "overexposed", which means that it should be much brighter. The scale under the picture gives the product of the opening's radius (in μm) times the deflection angle (in degrees).
A simple experiment:
A small hole is pierced into a piece of aluminium foil with a sewing needle. Look through this hole at a "pointlike" source of light, e.g. the reflected image of the sun in a small silvery glass sphere as used to decorate christmas trees. (In addition to the images shown below one may see in this experiment streaks in the vitreous body of one's eye; to see the diffraction image, it may help to move the piece of foil in front of the eye somewhat.)
One may also fasten the foil over a photographic camera's front lens to get pictures like the following:
Diffraction image of a nearly circular small hole pierced with a sewing needle into an aluminium foil, fixed in front of a digital camera's lens. The diameter of the hole is approximately 0.04 mm (about 0.002 in). A small low voltage incandescent bulb has been used as light source.
Left hand side: the exposure time was short so that the central spot is not overexposed.
Right hand side: The same with longer exposure time. The irregularities of the fringes show that the hole was not exactly circular.
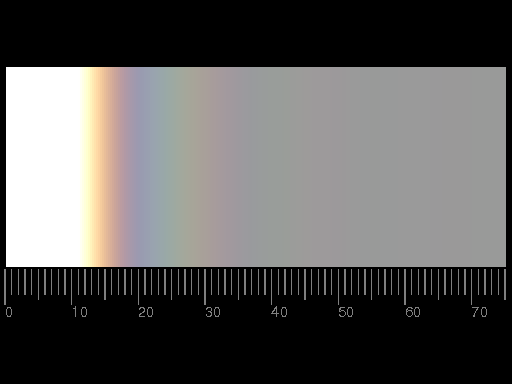
Computational result: left hand side:
The sequence of colours in the diffraction pattern of a circular hole. The scale below gives the product of the hole's radius (in μm) and the deflection angle (in degrees).
Right hand side:
The same with increased brightness. The "overexposed" part (which cannot be displayed correctly) has been shaded grey.
Of course, there are no diaphragms with circular holes floating in the air. However, the diffraction images of circular opaque discs are the same as those of circular holes. (More generally, Babinet's theorem states that "complementary" obstacles produce identical diffraction images.) Though the water droplets forming clouds are not opaque, for rough estimates the transmitted light may be neglected. If the droplets are so small that the first diffraction minimum occurs at an angle significantly larger than 0.5º then the finite extension of the sun's disc will not wash out the interference fringes. If the droplets all have nearly the same size, colours will be seen, in the ideal case in concentric rings forming an aureole around the sun.
Left: Moderately coloured aureole around the sun. To take this picture, a black plate of glass has been used as a mirror.
Right: On a cloudy day, it happens quite frequently that the sun may be seen faintly through some thinner part of the clouds. It is seen as a white disc, surrounded by a bluish aureole.
Some more pictures
In nearly all of the many pictures of aureoles and iridescent clouds shown on several websites, the part close to the sun is either shielded by some obstacle, or severely overexposed because of its dazzling brigtness. Therefore, it is rarely seen that the central part of the aureole is bluish.
Warning: Looking into the sun or close to it may cause severe and permanent damage of the eyes and must be avoided, even with sunglasses! A glass plate painted black on the back is suitable to observe sun aureoles. The plate has to be held in such a way that the mirror image of the sun cannot be seen.
If the droplets are small and all of approximately the same size, this phenomenon can be quite colourful.
Right: Aureole around the moon. Photo: Wiebke Salzmann. The central portion is over-exposed; if the mousecursor is over the image, the size of the moon is shown as a black disc. Sources: Wikimedia/Wikipedia,
license CC BY-SA 3.0.
| 
|
 | Aureoles or coronae can have other origins. As an example, on the left hand side an aureole around the sun produced by the curly fibers of a synthetic curtain fabric. The diameter of the fibers is about 0.02 mm.
|
Iridescent clouds and coronae around the sun or moon are essentially due to diffraction of the light on water droplets. However, there is actually no need to use approximate calculations, as the exact solution for the scattering (refraction, diffraction and reflection) of light by spherical droplets is known. This is dealt with in a special section.
Another phenomenon caused by reflection and diffraction of light may be seen on mountains or from airplanes when the own shadow is cast on mist, fog or clouds. This is the glory around the antisolar point, or in the case of the "Brocken spectre" around the shadow of one's own head. For the glory there is no intuitive simple explanation, but of course the
exact solution of the scattering problem yields it correctly.
Image: Glory, or airplane Brocken spectre.
Photo: "Brocken Inaglory" (
site),
Source:
Wikipedia,
license
CC BY-SA 3.0.
Dusty or fogged window panes, slight scratches in the glass etc. may be the cause of colourful diffraction effects. Particularly, reflecting surfaces are to be mentioned: a small plane mirroring area on an otherwise mat or dark surface will, in reflected light, produce diffraction patterns as does an opening in transmission.
Speckle
An inconspicuous example: on sunlit mat metallic surfaces one can see tiny coloured speckles:

|

|
|
The surface of a coin made of grey alloy looks speckled in direct sunlight. | Without direct sunlight, the same coin shows only dull grey.
|
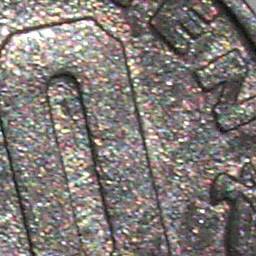
|

|
|
Looking closely or, here, zooming in, one can see that the speckles are coloured.
|
The same detail without direct sunlight only shows the roughness of the surface, but no colours.
|

|

|
Goethe in his treatise on colours (Farbenlehre) has given a fairly complete list of such and similar phenomena, which he called "epoptical",
"catoptrical" and "paroptrical colours":
"373. Läßt man ein poliertes Silber durch Scheidewasser dergestalt anfressen, daß das darin befindliche Kupfer aufgelöst und die Oberfläche gewissermaßen rauh werde, und läßt alsdann das Sonnenbild sich auf der Platte spiegeln, so wird es von jedem unendlich kleinen erhöhten Punkte einzeln zurückglänzen und die Oberfläche der Platte in bunten Farben erscheinen. Ebenso, wenn man ein schwarzes ungeglättetes Papier in die Sonne hält und aufmerksam darauf blickt, sieht man es in seinen kleinsten Teilen bunt in den lebhaftesten Farben glänzen."
["373. Etching a piece of polished silver by aqua fortis such that the copper contained therein gets dissolved and the surface becomes rough, and then observing the mirror image of the sun in this plate, one will see it glittering from every infinitely small protruding point and the surface of the plate will appear vividly coloured. Similarly, a piece of black non-glossy paper exposed to the sun, if observed carefully, shows its smallest parts shining in most vivid colours."]
The explanation of this effect needs some preparatory background.
It has already been mentioned that laser light is much more coherent than light coming from the sun or an incandescent bulb. Shining laser light on a mat surface, e.g. a piece of paper, it does not appear uniformly lighted but rather speckled. This is the same phenomenon as that mentioned above. But while it is rarely noticed in sunlight, this speckle pattern is very conspicuous with laser light and sometimes annoying. Of course, with monochromatic light, no additional colours can occur.
Left: A sheet of white paper, partly covered by a transparent ruler (with millimeter-scale) in the light of a laser pointer, the light of which has been fanned out by a lens.
Right: The same grey coin as above, now in the light of a laser. The diameter of the coin is 21.2 mm. The glittering of the speckles cannot be reproduced in the images.
The speckle pattern is constant in time, it changes when the observer moves (or the light source or the object is moved). It is remarkable that the speckles are seen sharply, regardless whether the eyes are focused to the surface or not. Looking at them through a magnifying glass, they don't increase in size, but in number.
It is somewhat simpler to discuss the phenomenon for the case when the eye (or the camera) is out of focus with respect to the object looked at. Let us first consider this case. Light coming from one point will shine on an approximately circular area on the retina (or film/sensor), and correspondingly all rays arriving at one point of the retina will originate from a small, circular area. If this area is illuminated with coherent laser light, the relative phases of the different waves meeting at the retina will be constant in time, the waves will interfere constructively (enhancing each other) or destructively (weakening or extinguishing each other), depending on finest details of the surface.
The size of the circular area sending light to one point of the image depends on the aperture of the iris. Smaller aperture leads to coarser speckle, as shown in the following photographs:
 |  |
Laser speckle. Photos taken with aperture f:3.5 (left) and aperture f:8 (right). |
One might think that speckle should vanish if the object is in focus, as then each point is mapped to one point of the image – but this is only the geometrical optics idealization. Wave optics tells us that a point is imaged to a small diffuse spot, due to the finite aperture of the objective. Neighbouring spots are overlapping, and again there is interference – speckle instead of uniform lightness.
The colours of the sunlight speckles on mat metallic surfaces etc. mentioned in the beginning are due to the dependence of the speckle pattern on the wavelength of the light. The wavelengths which we perceive as red produce a different pattern as those which are seen green and the blue ones still another one. The superposition of all of them is varicoloured.
This can be worked out a little bit more in a simplified example. Consider a small element, a plane micro-facet of the mat surface which mirrors light to the eye. Due to diffraction, the reflected light spreads, and if the facet is small enough, only part of the reflected (and diffracted) light enters the eye and is focused onto the retina. From the center of the reflected pencil of light outwards, the sequence of colours will be similar to that shown above for a circular aperture. These colours are shown below with maximum brightness. Depending on the viewing angle, the facet may show any of these colours.
Plane facets are not necessary for the speckle pattern to appear. However, for an arbitrary rough surface, a detailed description is neither feasible nor does it make sense.
 |
Speckle pattern can also occur on hairlike objects: spider web strands seen in backlighting, or, as in the picture to the left, on the parachute hairs of plant seeds. In photographs this is best seen on fibres somewhat out of focus.
Image: dandelion blowball, seedhead of Taraxacum officinale. Click on the picture for enlargement!
|
More diffraction- and interference phenomena are presented in the sections on
soap bubbles etc., on
iridescence and lustre and on optical phenomena on spider webs.
Back to the index page The origins of colour
Legal Information Data Privacy