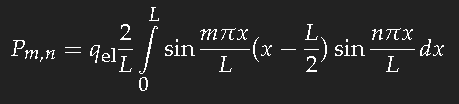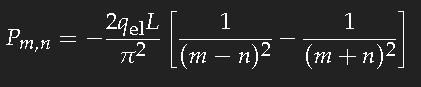The html formatting and custom instructions have been disabled on this server. The same file with adapted formatting can be found here: https://farbeinf.de/static_html/dyes.html.
Colourants are substances which give colour to the objects which contain them, e.g. flowers, leaves. Dyes in a broad sense are coloured and water-soluble. In narrow sense, a dye is a colourant which can be used to dye textile fibers, which means that it has an affinity to the material to which it is applied (so that it is not easily washed out) and, moreover, gives the desired colour already in very small concentration. Pigments are water insoluble, powdery substances, e.g. finely ground minerals, used to produce paints and lacquers with some bonding agent like linseed oil, gum arabic, or resins.
Why are dyes so strongly coloured? To find the answer, let us first look at the chemical structure of some of them (in broader sense).
 | Indigofera heterantha Brandis, the indigo shrub which looks very similar to
Indigofera tinctoria L., the indigo plant used for dyeing. The green colour is – as in all green plants – due to plenty of chlorophyll in the leaves, the pink colour of the flowers due to a colourant belonging to the group of anthocyanes to be dealt with later. The blue dye named indigotin which is obtained from I. tinctoria is itself not present there, instead there is the almost colourless (yellowish) precursor indican. In the process of dyeing, indican is first converted to indoxyl which by oxidation afterwards is converted to indigotin. |
Chlorophyll
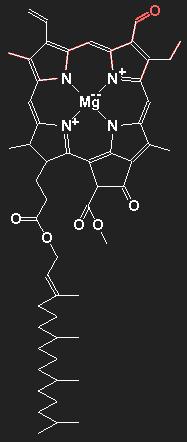 | |
Chemical structure of chlorophyll a (without the red part) and chlorophyll b (with the red appendix).
The main constituents of organic matter are carbon and hydrogen. The lines stand for covalent chemical bonds, thus each line represents a pair of electrons. Double lines mean double bonds. The carbon atoms themselves are not shown; at each end-point, kink or vertex there is one carbon atom, if there is no other chemical symbol. In addition to carbon and hydrogen, nitrogen N, oxygen O, and magnesium Mg are present in the molecule. The hydrogen atoms, including the bonding electrons, are also not drawn. If there are less than four lines emerging from a carbon-site, there is a bound hydrogen atom for each missing line. Thus, a line ending represents a CH3-group. Chlorophyll b differs from chlorophyll a by the replacement of a methyl group / by a formyl group /=O.
|
Anthocyanins
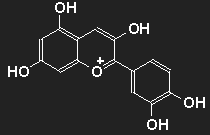 | | Cyanidin as an example for the group of anthocyanins. By removal of OH units present here or by addition of more OH or OCH3 units many different colourants in the range of blue, violet, purple and red are obtained. |
 | |
The cornflower Centaurea cyanus L. is blue due to cyanidin.
|
Carotene, carotenoids
Carotenoids are contained in many fruits and vegetables. The orange carotene present in leaves aid photosynthesis by transmitting the energy absorbed from light to chlorophyll. Red, orange and yellow colours of flowers, fruits and vegetables are due to carotenoids.
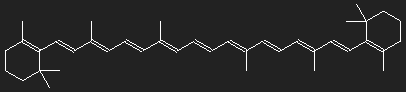
Structure of β-carotene (provitamin A). Carotene consists only of carbon and hydrogen.
Indigotin
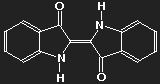
Indigotin
Structural formulas do not show the exact positions in space – the three-dimensional arrangement is drawn in a plane and is thereby distorted. They are used to display the bonding. But even in this respect, it is difficult to give a good picture of reality.
Notice the considerable number of double bonds. In most cases, along longer paths there are alternating single and double bonds. This is, as we shall see, important to allow absorption of photons and thus for colour.
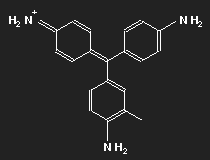
Fuchsine
 |
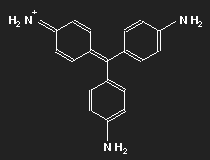 |
| Fuchsine | Parafuchsine |
Historically, after mauvein, fuchsine is the second dye that has been synthesized. It has been named after the fuchsia, a plant with pink flowers, and is also known as magenta or rosaniline. In most cases a mixture of similar substances, fuchsine and parafuchsine in particular; the structure of the latter is more symmetric.

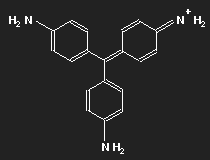
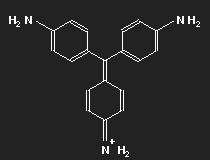
Let us consider parafuchsine. It is a positive ion. Given the spatial arrangement of its constituents, and taking account of the chemical valences, a structure equation as shown in the left picture above results. Or the middle one – or the right one. Actually, the three forms are identical and can be transformed into each other by rotation. The nitrogen on the left side carries positive charge – or that on the right side – or that at the bottom.
In fact, nature does not discriminate between these three possibilities: the state with lowest energy is a superposition of all three of them. In this state, there is no electronic motion within the molecule (otherwise radiation would be emitted). We encounter here again the peculiarity of quantum mechanics which makes it difficult – or rather impossible – to understand it in familiar concepts. An indivisible particle can be distributed to different places.
It follows for the alternating double bonds that they likewise are not well localized (as the structural formulas might suggest), but are "delocalized". This is a well known fact in the example of the benzene ring: all bonds between the six C-atoms are the same; often the benzene ring therefore is denoted by a simple hexagon with inlying circle.
Charge transfer
To simplify the discussion we first consider a fictitious molecule or ion which offers two distinct locations for an electron. The quantum mechanical ground state then would be
|g⟩ = |left⟩ + |right⟩.
The superposition
|u⟩ = |left⟩ – |right⟩
is also an eigenstate with somewhat higher energy
Eu. According to quantum mechanics its time dependence is
exp(–2πiEut/h)
( h ist the Planck constant). This "trivial" time dependence means that the state is stationary, all measurable quantities are time-independent if the system is in this state. There is no motion.
Motion results when states with different energies are superposed, as an example the states |g⟩ and |u⟩ with equal weights. After some simple algebra one obtains a result which may be brought in such a form which obviously shows an oscillation between the states |left⟩ and |right⟩ or, in other words, that the charge moves forth and back – along the path formed by alternating double and single bonds there must be an electric current!
The transition from state |g⟩ to the excited state |u⟩ can go along with the absorption, the reverse transition with the emission of a photon. One can imagine that during the absorption or emission process, the system is in a superposition of ground and excited state so that the charge oscillates with the appropriate frequency to and fro. Such a charge transfer over several atomic distances goes along with large absorption and emission probabilities.
In the case of three different sites where the charge can be concentrated (like in parafuchsine and fuchsine) the discussion is a little bit more involved. With simple model assumptions and a little algebra one gets the (non-normalized) states
|g⟩ = |1⟩ + |2⟩ + |3⟩,
|u1⟩ = 2 |1⟩ – |2⟩ – |3⟩ and |u2⟩ = |2⟩ – |3⟩.
Qualitatively, what has been said above remains valid.
A model for gross estimates
Differently shaped chains with alternating single and double bonds are found in different dye molecules. In the simplest cases they are more or less straight, only slightly notched. Consider carotene as an example. Let us ignore for simplicity the ring structures at the ends as well as the CH3-groups attached to the chain, may be that their function is only to provide handles for their manipulation by the molecular machines and that their influence on optical behaviour is small. To obtain a gross estimate, we ignore all details of the structure.
We suppose that the nonlocalized electrons of the double bonds are responsible for the strong absorption of light, and as a first step we think all of them to be removed. What remains is a chain of 22 carbon atoms bound together with simple bonds. On both ends, there are two H-atoms, all other C-atoms have one bound H-atom each. For every double bond two electrons have been removed, thus every C-atom has one positive charge unit in excess. This is the inert skeleton of the dye molecule, and for our model we replace it by a narrow long potential well or box potential. This box has now to be filled with the electrons which we had removed. The interaction of the electrons is neglected.
Now the Schrödinger equation should be used to determine the wave functions. We assume that the shape of the wave functions perpendicular to the long axis of the box are all the same and need not consider these directions any more. Thus the task has finally been reduced to the one-dimensional potential well with hard walls containing freely moving electrons.
For this case we already know the solutions of the Schrödinger equation: the wave functions have the same shape as the normal modes of a vibrating string. Since the electrons move freely within the box, the relations between wavelength, momentum and kinetic energy of free particles hold: p = h/λ, E = p2/(2m).
(p is the momentum, λ the wavelength, h the Planck constant, E the energy and m the mass of the electrons.)
The length of the box is denoted by L. The solutions of the Schrödinger equation are standing waves with wavelengths 2L, L, 2L/3, L/2, etc., i.e. 2L/n, where n = 1, 2, 3 ... The quantum number n is simply the number of the single-particle state. The corresponding energies are En = h2/(8 m L2) n2.

Density distribution of an electron in a long box with impermeable walls. Shown are the lowest-energy seven states, the ground state at the bottom. The number of clouds, into which the electron distributes itself, is equal to the quantum number
n.
Each of the states which we have obtained can only hold two electrons with opposite spin, according to the Pauli principle. If 22 electrons have to be accommodated, then in the ground state the level n = 11 contains two particles, whine the level n = 12 is empty. By the action of an electromagnetic wave, an electron can be lifted from level 11 to level 12. For this, an amount of energy ΔE = E12 – E11 is needed; in other words: photons carrying this energy can be absorbed.
Using the equation E = h ν = h c/λ, which holds for photons, the wavelength λ corresponding to the absorption maximum is obtained.
Chosing for the length L the number of carbon atoms multiplied by the typical distance between two neighbours (which in chains with alternating single and double bonds is about =0.139 nm, this corresponds to a stretched chain. The fact that consecutive bonds form an angle of about 120º is accounted for by multiplying the stretched length by a factor of 0.866 to obtain the effective Length. (0.866 is the height of an equilateral triangle with unit sides.)
For a single-particle transition from level 11 to level 12, the necessary photon energy corresponds to a wavelength of 1006 nm, this not in the visible range, but in the infrared. In spite of all model assumptions and approximations – an absorption maximum of carotene in the infrared is to be expected.
Is it possible for carotene to absorb photons with higher energy? This would correspond to transitions not between subsequent levels, but between more distant levels. The transitions from n = 10 to n = 12 or from n = 11 to n = 13 are impossible for symmetry reasons. For the transition from n = 9 to n = 12 we obtain λphoton = 367 nm, a wavelength in the ultraviolet region somwhat beyond the end of the visible spectrum.
Apparently the model is too gross and the omitted appendices probably have more influence than we anticipated.
The model reproduces the basic assumption that the electrons which form the double bonds can freely move over the whole chain of alternating bonds: the density of each of them is distributed over the whole chain. The chain with alternating single and double bonds thus is analogous to an electric conductor, like a minute metal wire.
The conduction electrons in a piece of wire (antenna) can be excited to perform periodic oscillations by electromagnetic waves. The resonance frequency is the higher the shorter the wire is. The connection between length and resonance frequency is quite general and well known from vibrating strings, organ pipes etc. The quantum mechanical model which we consider is no exception. The lowest (and most easily excited) oscillation frequency was obtained lower than the frequencies of visible light; one can expect that for somewhat shorter chains it will be obtained within the visible range.
Let us try one more estimate for a somewhat shorter chain.
Carotene (provitamin A) can be transformed to vitamin A by the body, this is the precursor of retinal which is the light sensitive part of visual purple (rhodopsin). Visual purple consists of a large opsin protein to which retinal is bound. The structure formula of retinal clearly shows the close relationship to carotene.
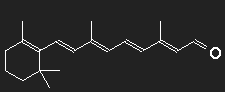
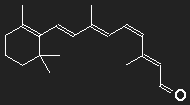
Left: All-trans retinal, right: 11-cis retinal,
below for comparison once more β-carotene

Cut
β-carotene in the middle, replace one half of it by an oxygen atom – and you got retinal (at least with pencil and paper).
Subtle details are beyond the scope of the model; we ignore the kink of the chain as well as the fact that there is an oxygen atom instead of CH2 at the end.
Consider a box with length corresponding to 12 C atoms to be filled with 12 electrons. For the lowest excitation an electron has to be lifted from the 6th to the 7th single-particle level, the energy necessary for this corresponds to the wavelength λphoton = 529 nm.
The absorption maximum of visual purple is approximately at 500 mn! – It is rather an accident that we came so close to that number. However, it is important that we got the right order of magnitude.
What has to be done in a serious computation of a molecule's colour?
Exact calculations of molecular properties are not possible, one has to resort to approximate numerical methods. A common feature of all of these is the use of a fictitious (or effective) potential (which also accounts for the mutual interaction of the electrons) to generate electron wave functions. The potential depends on the distribution of the electrons in space – which is the desired result. So one starts with a guess of the density, from this one computes the potential which then leads to a new density distribution. This procedure is repeated until the result agrees sufficiently well with the input. (There are different variants of such Hartree-Fock and energy-density-functional methods.)
There are more complications: it is not sufficient to deal with a single molecule, one has in addition to consider the surroundings. Electric forces are long-ranged, therefore the neighbourhood has noticeable influence. It is not simple. Such computations became only possible with powerful computers.
Fortunately, chemistry did not depend on such computations; the first artificial dyes (mauveine, fuchsine) have been synthesized long before quantum mechanics was discovered. But today quantum mechanics allows us to understand the empirical rules of colour chemistry.
Modifying the potential
To estimate how electric charges (ions) in the vicinity of a dye molecule influence its colour, we again consider the box model, and in particular the transition from the single-particle level nr. 6 to level nr. 7. The figure below shows again the respective density distributions. We now introduce a shallow potential step in the middle of the box as drawn in the lower part of the figure, which is supposed to be much lower than the energy difference of the two levels in question. The density of one of the states has a maximum at the potential step while the density of the other one avoids this region. The energy of both states will be somewhat increased, but the upper state will be affected more than the lower one, which means that the energy difference between the states becomes larger.

Potential box with a flat step in the middle (lowest image) and on top of it the density distributions of an electron in the states number 6 and 7.
This means that the absorption maximum will be shifted towards shorter wavelengths.
If on a chain of alternating single and double bonds an H-atom is replaced by an other atom, an OH-, CH3- or some other group, this introduces a local change in the effective potential which can have a similar effect.
An example:
 |
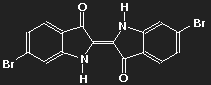 |
Indigo
(colour of plant extract applied
to paper or cotton) | Purple (6,6'-dibromoindigo)
(colour of Tyrian Purple) |
The potential where the delocalized electrons move depends on the distribution of all charges in the molecule, which is changed when hydrogen is replaced by bromine.
Width of the absorption curve
Atomic spectra are called line spectra because in a spectroscope they appear as a sequence of lines. The lines are images of the spectroscope's entrance slit, the location of which depends on the wavelength. High resolution spectrometers reveal that the lines are not sharp in the sense that they correspond to a single frequency or wavelength, but have a small, but finite width.The theoretical lower bound to the line width, called "natural line width", is never reached in the visible region. The observed width is due to thermal motion and the Doppler effect and the so-called collision width.
In a collision two molecules come close to each other. The interaction with the collision partner is equivalent to an additional field of force, attractive or repulsive, which leads to displacement of energy levels during a short time interval. These statistically distributed changes of the transition frequencies produce the collision broadening in a not too dilute gas.
The spectra of molecules differ significantly from atomic line spectra. We consider first the simplest case of a two-atomic molecule. The "dumb-bell shaped" thing can vibrate and rotate. Typical energies of vibrations and rotations are much smaller than the energies needed for electronic excitations. Vibrations are slow compared with electronic motion. Roughly speaking this means that a vibrational state may persist while an electronic transition occurs. Semi-classically, the energies of the molecular electronic levels would depend on the distance of the nuclei, they depend on the vibrational state of the molecule. Thus, not only one energy, but a discrete sequence of different energies (and wavelengths) is observed in the spectrum for a given electronic transition. The same arguments hold for the rotational states which lead to still finer structures: instead of single lines there are vibrational and rotational "bands".
Polyatomic molecules exhibit rich vibrational spectra. In addition, the larger the molecules are, the more dense are the rotational energies. Due to the finite width of the lines they overlap and cannot be resolved any more. Immersed in a liquid or part of an organic structure, the molecules exchange energy with their neighbours due to thermal motion, and this holds even more. Instead of single emission or absorption lines, large molecules have absorption curves with very broad peaks. Emission spectra are observed only in the exceptional case of fluorescence.
Fluorescence and related phenomena are dealt with in a separate section "Luminescence".
Strength of absorption: the dipole moment
 | |
The berries of pokeweed contain a magenta-coloured dye in a concentration which makes them black. The dye can absorb visible light of all wavelengths; the absorption maximum is in the green region. In the stalk the concentration is very low, but this gives a vivid purple colour. What is the reason for the strong absorption of light by dyes?
Asiatic pokeweed (Phytolacca acinosa Roxburgh)
|
If an electric charge is accelerated it emits electromagnetic radiation. Comparatively simple to deal with is the case of an oscillatory periodic motion with constant frequency, when the amplitude of the motion is small compared to the wavelength of the emitted radiation. On the other hand, an electric charge which is bound by some "elastic" force to its resting position can be forced to oscillate by an electromagnetic wave; the energy of the oscillation is taken from the wave, i.e. radiation is absorbed.
The quantity which determines the amount of radiation emitted by an oscillating charge is the dipole moment. This is the product of charge times oscillation amplitude. Absorption is determined by the polarizability which is defined as the dipole moment induced by an electric field of unit strength. It is the square of the dipole moment or, respectively, polarizability which is of importance. Thus, a ten times larger dipole moment means hundred times more radiation.
The expressions for the probability to emit or absorb a photon contain the square of the transition matrix element of the dipole operator, which in quantum mechanics corresponds to the classical dipole moment. In spite of its complicated name we can get an estimate of this quantity if we know the size of the molecule in question.
For the simple model of a long box-potential (length
L) it is easy to calculate the dipole transition matrix element
Pm,n, and we can take this value as a good estimate of that quantity for a chain of conjugate double bonds of the same length. For the transition of an electron from the single-particle state
n into the state
m one has to evaluate
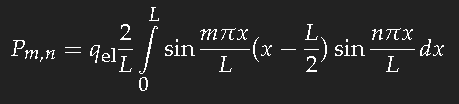
(
qel ist the charge of the electron.) This is not difficult. If
m–n is an even number, the result is zero; for an odd value of
m–n one obtains
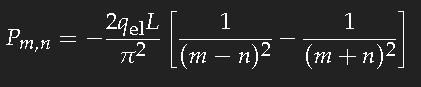
which yields for the transition between consecutive states approximately 20 percent of the length
L multiplied with the electron charge. (The sign is unimportant as the square of this expression is needed.)
Crude as it is, this estimate gives an approximate value even for a single atom, if instead of
L the diameter of the atom is taken, which roughly equals the distance of two atoms in a chemical bond.
The delocalized electrons along a chain of alternating double and single bonds are primarily responsible for the absorption of light and thus the colour. Therefore, the corresponding part of a dye molecule is called the chromophore, "colour carrier", or chromogene, "source of colour". Building blocks of the molecule which can easily supply or accept electrons (electron donators and acceptors) located at the outer ends of the chromogene increase the values of dipole matrix elements and are called auxochromes, "colour intensifier". The NH2-groups of fuchsine may serve as an example.
Remains to discuss the different kinds of dye, chemical aspects of colourant synthesis and the dyeing process. This will not be done here. Information on these topics is provided by various websites. As an example one on colour chemistry (in German).
Pigments


Pigments in a store for artists' supplies. From left to right: permanent light yellow, yellow ochre, iron oxide red (English red ?), iron oxide yellow, raw sienna, chrome green.
You may find in the Web compilations of origin and historical development of anorganic pigments, listings of common pigments which are used for painting and production of paints and inks, and of the chemical composition. A good starting point for the search is Wikipedia. I do not want to duplicate this and only note the most distinctive difference between pigments and dyes:
The picture above shows it: while dyes in minute quantities already give strong colours, volume and weight of pigments are not negligible.
This is not only of practical importance, it also means that for a theoretical understanding a different approach will be necessary. For a dye it makes sense to investigate a single molecule, but for a pigment one has to find the colour of a tiny crystal. Though its size is only that of a grain of dust, on an atomic scale it is huge. This is the topic of a special section on coloured crystals and minerals.
Back to the index page "the origins of colour"
Legal Information Data Privacy