Zufallsbeobachtungen

Das annähernd waagerecht zwischen Stauden gespannte Radnetz einer kleinen Spinne wird vom leichten, verwirbelten Wind bewegt und glänzt und glitzert vor dunklem Hintergrund in der Sonne. (Sonnenhöhe zu diesem Zeitpukt ca. 19°.) Der Durchmesser des sehr regelmäßigen Rades beträgt ca. 10 cm. Die Spinne habe ich auch gesehen, konnte sie aber nicht fotografieren. Sie war winzig, Körperlänge kaum mehr als 1 mm. Vermutlich eine junge Kreuzspinne (Araneus diadematus).

Farben an Radnetzen von Spinnen habe ich schon früher beschrieben [1], [2], da erfolgte die Beobachtung aber im Gegenlicht, also in geringem Winkelabstand von der Sonne. Die Streuwinkel betrugen daher nur wenige Grad. Diesmal aber war der Winkel zwischen einfallenden und gestreuten Strahlen ungefähr 40° bis 50° groß; der Eindruck war daher eher der, dass das Licht an den Fäden des Spinnennetzes reflektiert wurde.

Das überbelichtete Blatt im Hintergrund stört etwas. Mit Änderung des Blickwinkels ändert sich jedoch das Erscheinungsbid des Netzes.

Die Glanzstellen an den straff gespannten Radialfäden unterscheiden sich deutlich von den zahlreichen kleinen Reflexen an den klebrigen vom Wind bewegten und gekrümmten Fangfäden.

Es fällt auf, dass die Fangfäden unterschiedich hell glänzen und auch verschiedene Farben zeigen. Das ist an einer verwackelten Aufnahme noch deutlicher zu sehen:

Die dünnen Fangfäden tragen in regelmäßigen Abständen Klebetröpfchen. Die sind aber so klein und so dicht beisammen, dass sie nicht getrennt gesehen werden. Es glänzen also die Fäden und die Tröpfchen, und die Lichtwellen von diesen beiden haben etwas verschiedene Wege zrückgelegt, wenn sie das Auge erreichen. Es ist also so ähnlich wie bei Seifenblasen, wo die von der Ober- und der Unterseite der Lamelle reflektierten Wellen interferieren und so farbige Reflexe erzeugen.

Auf der linken und der rechten Seite des Netzes glänzen die Fäden deutlich weniger hell und auch noch in anderer Farbe als vorne (im Bild unten) und hinten. Meine Erklärung dafür ist, dass durch die Klebetröpfchen ein großer Teil des zwischen den Tröpfchen liegenden Fadens teils beschattet und teils verdeckt wird und somit nicht zum Reflex beiträgt. Die Dicke der die Fäden umhüllenden Klebeschicht variiert zwischen den Tröpfchen, in der Mitte befindet sich meist eine Verdickung, so dass der Wegunterschied der an Faden und Tröpfchen reflektierten Strahlen nicht konstant ist.

Nebenstehend ein Ausschnitt aus der linken Seite des zweiten Bildes. An den vom Wind gekrümmten Fangfäden siegt man außer der Glanzstelle auch noch die Beugungsbilder erster Ordnung, die an einigen Stellen oberhalb der Bildmitte Spektren von Blau bis Rot zeigen. Unterhalb der Bildmitte nur noch die blauen Anteile des Beugungsbildes. (Zum Vergrößern darauf klicken!) Je nach der Orientierung und Krümmung der Fäden sind die Beugungsbilder – wie auch die Reflexe – an den einzelnen Fäden größer oder kleiner oder eben nicht zu sehen.

Der blaue oder auch grüne Glanz der Fäden ohne helle Reflexe lässt sich somit als Teil des Beugungsbildes erster Ordnung an den periodichen Strukturen verstehen.

Schmelzendes Eis

Das Eis auf einem Baggersee ist bereits am Auftauen. Der strahlend blaue Himmel spiegelt sich darin, und man sieht durch das Eis auf dem niedrigen Wasser den sandigen Untergrund.

Beim Abschmelzen (oder Abdampfen?) haben sich zwischen den einzelnen Einkristallen Rillen gebildet, die die Kristallgrenzen deutlich sichtbar machen. Überraschend, dass, je nach Blickwinkel, einzelne dieser Rillen im Sonnenlicht glitzern. Nicht die ganze Breite der Rille, sondern nur eine der beiden Flanken, die einen ansonsten nicht glitzernden Einkristall umrundet. In den Rillen haben sich offenbar mikroskopisch kleine Facetten ausgebildet, deren Orientierung durch das Kristallgitter bestimmt wird und daher für den ganzen Saum gleich ist.

Sehr seltsame Interferenzfarben auf Eis, zweiter Versuch

Im Mai 2018 beschrieb ich diese Beobachtung von Mika-Pekka Markkanen und brachte einen Erklärungsversuch, allerdings unter großen Zweifeln.

Ein zugefrorener Moorsee irgendwo im Norden von Norwegen, auf dem neben der hellen Lichtstraße farbige Interferenzstreifen zu sehen sind.

„Beim Schlittschuhlaufen auf einem Moorsee bemerkte ich diese farbigen Bögen beiderseits der hellen Sonnenreflexe. Wie man sieht, stand die Sonne ziemlich tief, und das Eis glänzte unglaublich stark, aber obwohl ideal fürs Schlittschuhlaufen, war es doch voll von kleinen Rissen und den verschiedensten Oberflächenstrukturen […] Diese Erscheinung war während der Bewegung zu sehen, ohne Kamera, Sonnenbrillen oder Polarisationsfilter, sogar auf einem I-phone-Video ist sie zu bemerken …“

Das ist, frei übersetzt, was Mika-Pekka Markkanen schrieb als er mich fragte, ob ich diese Erscheinung kennen würde. Aber so etwas habe ich noch nie gesehen, und ich glaube auch nicht, dass viele andere das schon kennen.

Den Erklärungsversuch kommentierte ich damals: „Die verwendeten Parameter lassen sich nicht aus der hexagonalen Symmetrie der Schneekristalle herleiten, dies ist ein großer Nachteil und zeigt, dass noch nicht die richtige Erklärung gefunden wurde. …“

“Not a scientist here, but I have observed the rainbow effect on ice in the arctic on many occasions. (I have worked in the Alaskan arctic for many years)

I always associated it with the the presence of diesel generators and assumed that it was the result of a fine layer of oil deposited on the surface downwind from the exhaust of the large generator units or in some instances diesel haul trucks. I noted that I was unlikely to see it when many miles from the vicinity of such pollution...

Perhaps it is not the oil, but the fine particles of ice formed from the exhaust?

Just an observer.

Ray D. Congdon - KL7UT
Retired Telecommunications Technician”

Partikeln, also z.B. Rußteilchen, die auf dem Eis liegen, könnten Farben hervorrufen, queteletsche Ringe oder Streifen. Dadurch kann ich jedoch das einfache geometrische Muster nicht erklären. Das gilt auch für winzige Eisteilchen. Etwas größere Eisteilchen – Schneekristalle – könnten Spektralfarben hervorrufen, aber die unterscheiden sich von den typischen Interferenzfarben und müssten Ringe um das Spiegelbild der Sonne bilden. Daher scheint mir ein sehr dünner Ölfilm wahrscheinlicher. Allerdings sieht man auf der Eisfläche im Vordergrund keine Farben. Ein zusammenhängender Ölfilm sollte auf dem Eis doch so ähnlich aussehen wie auf nasser Straße, diesen Fall kann man ausschließen. Aber man kann sich vorstellen, dass kleine Öltröpfchen, wenn sie vom Wind über das Eis geweht werden, bevorzugt an winzigen steileren Stellen hängenbleiben.

Das erste Bild in der Reihe unten zeigt, an welchen Stellen die Sonne sich spiegelt, wenn die Flächenelemente nicht geneigt sind (nur ein Punkt), um 3.5° geneigt sind (entlang der kleineren Kontur) oder um 8° geneigt sind. (Die Sonnenhöhe beträgt hier 10°, dies ist auf den Fotos auch näherungsweise der Fall.) Vergleicht man dies mit den Fotos, so sieht man, dass die meisten Facetten, die zur Lichtstraße beitragen, um weniger als 3.5° geneigt sind, aber ein kleinerer Teil weist Neigungen bis ca. 8° auf. Zufällig orientierte, um bis zu 8° geneigte Oberflächenelemente können aber nur Reflexe innerhalb der 8°-Kontur hervorrufen, auch wenn man eine zweite Reflexion berücksichtigt, und aus dem Bereich, wo die Farben gesehen werden, kommt in diesem Fall kein Licht zum Auge. Es müssen also Oberflächenelemente vorhanden sein, die so steil sind, dass sie nicht zur Lichtstraße beitragen, die aber das schon einmal reflektierte Licht in einen größeren Raumwinkelbereich reflektieren. Das zweite Bild unten zeigt, wo zweifach reflektiertes Licht gesehen wird, wenn zufällig orientierte Facetten mit 3.5° und mit 60° Neigung vorhanden sind (graue Fläche). Man beachte, dass der höchste Punkt dieses Bereiches tiefer liegt als der Horizont. Das stimmt schon einmal mit den Fotos überein. Aber Farbe entsteht auf diese Art noch nicht.

Farbe entsteht, wenn sich an den steileren Facetten ein dünner Ölfilm befindet. Unter Einfluss der Adhäsionskraft zwischen Öl und Eis, Oberflächenspannung und Schwerkraft könnte sich das Öl dann am Rand der winzigen Erhebungen oder Stufen so sammeln, wie auf dem dritten Bild in der Reihe unten skizziert. Die Farbe, die durch die Interferenz des an der Oberseite des Ölfilms mit dem an der Grenzfläche zwischen Öl und Eis reflektierten Lichts entsteht, hängt von der Dicke des Films und dem Reflexionswinkel ab, und wenn wir annehmen, dass die Filmdicke mit der Steilheit der Fläche abnimmt, so kann man schließlich, mit ein paar plausiblen Annahmen über die Geometrie, ein Bild wie das letzte in der Reihe erhalten.

Die Wahrscheinlichkeit, dass ein Lichtstrahl nach der ersten Reflexion eine steilere Flanke trifft, ist umso größer, je flacher der Strahl verläuft. Ohne zu versuchen, die Eisfläche zu modellieren, kann man dies berücksichtigen, indem man für die erste Reflexion eine geeignete Wahrscheinlichkeitsverteilung für die Orientierung des Flächenelementes annimmt, im einfachsten Fall, dass man wie hier eine gleichmäßige Verteilung in einem vorgegebenen Raumwinkelbereich wählt.

Die Abhängigkeit des Reflexionskoeffizienten von Polarisation und Einfallswinkel wurde nicht berücksichtigt, es wurde ja nur eine grobe Abschätzung versucht, um die Ursache dieser Erscheinung zu finden. Eine korrekte Rechnung mit Hilfe der Fresnelschen Formeln würde die relativen Helligkeiten der einzelnen Farbbänder ändern, sehr wahrscheinlich das äußerste weiße Band stark abschwächen.

Regenbogenwurm

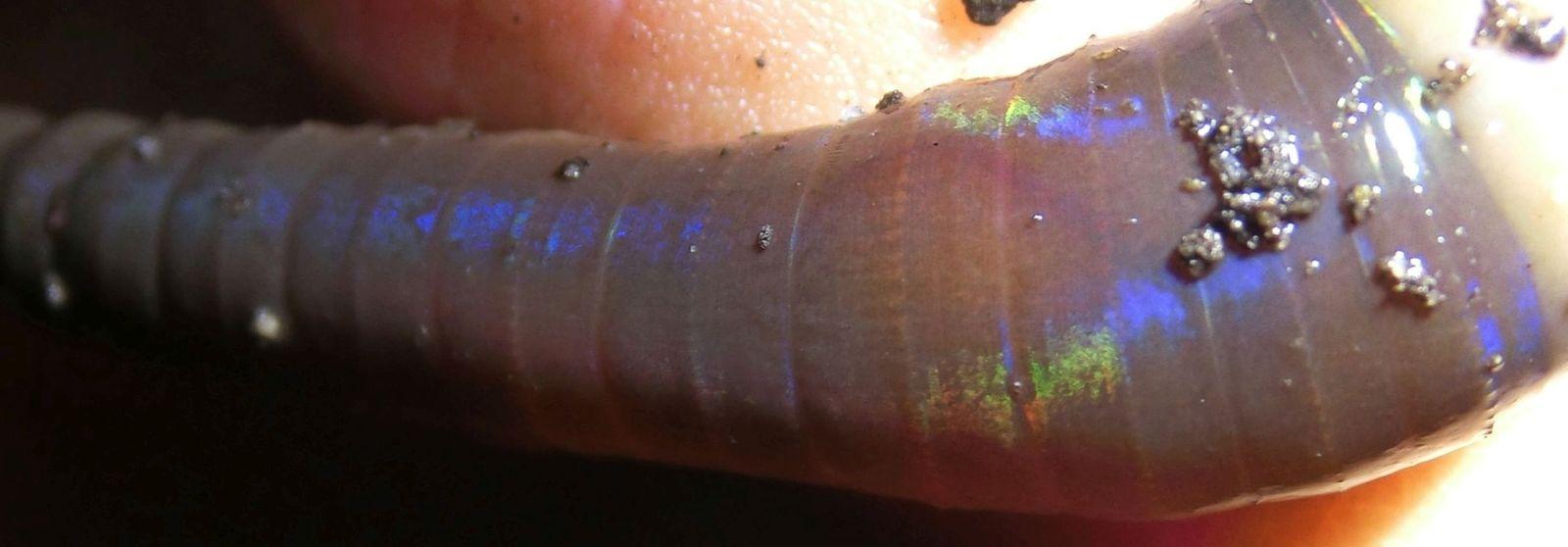
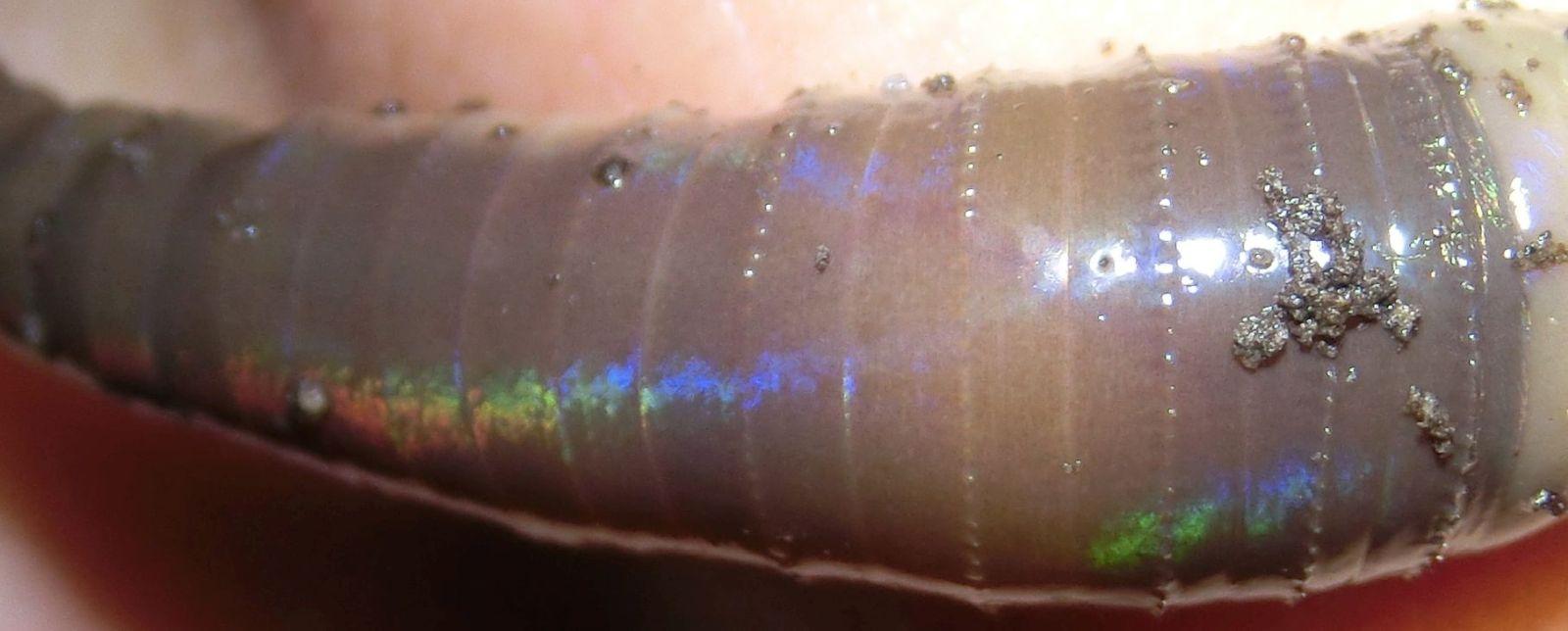
Bei Gartenarbeiten befördert man bisweilen einen Regenwurm ans Licht. Und wenn die Sonne scheint, dann kann man den Wurm auch schillern sehen. Ich erinnere mich, das schon vor vielen Jahren beobachtet zu haben, als ich noch nicht die Möglichkeit hatte, es durch Fotos zu dokumentieren. Fleisch schimmert ja auch manchmal grünlich oder rötlich; es wird wohl so ähnlich zu erklären sein, dachte ich damals und wunderte mich nicht sehr darüber. Später habe ich einmal gelesen, dass das Schimmern durch die Borsten des Wurms hervorgerufen würde; wo ich das gelesen habe, weiß ich nicht mehr.

Da ich in der letzten Zeit nur noch selten im Garten grabe, konnte ich diese Erscheinung noch nicht fotografieren. Aber vor kurzem hat mir Aleksandr Berdnikov ein paar Bilder geschickt. Über das Schimmern schreibt er "I’ve seen it attributed to tiny bristles", scheint das aber zu bezweifeln.

Das sieht sehr rätselhaft aus. Aber das folgende Bild, wo sich der Wurm um einen Finger ringelt, gibt einen Hinweis auf die richtige Erklärung:

Das erinnert an die Beugung an einer CD. Die farbigen Reflexe treten dort auf, wo bei gröberer Struktur eine Lichtstraße verlaufen würde. Also versuche ich eine Sruktur zu finden, die die entsprechenden Lichtstraßen liefert. Die Form des sich um den Finger windenden Wurms wird durch eine Torus angenähert. Auf diesem Torus sollen sich glänzende Linien befinden, die Glanzstellen sieht man dort, wo der Lichtstrahl von der Sonne mit der Linie den gleichen Winkel einschließt wie der Lichtstrahl von der Linie zu Auge, genauer gesagt: wenn sich die beiden Winkel nur wenig unterscheiden. Die Parameter wurden so gewählt, dass das Bild oben rechts ungefähr zu dem links daneben passt. Die beiden Lichtstraßen kreuzen sich an der Stelle, wo man das Spiegenbild der Sonne an der Torusfläche sähe.

Anatomische Details

„Nach außen hin ist der gesamte Körper des Wurms und damit auch jedes seiner Segmente durch einen Hautmuskelschlauch abgegrenzt. Auf eine einschichtige Epidermis, die einige Drüsen- und Sinneszellen enthält und nach außen von einer kollagenhaltigen Cuticula umgeben ist, folgt eine Ringmuskelschicht. An diese schließt wiederum nach innen die dicke Längsmuskelschicht an“ (Wikipedia).

„Die Leibeswand der Oligochaeten ist ein typischer Hautmuskelschlauch. Die Epidermiszellen sind zu einem einschichtigen Epithel angeordnet, in das Drüsen- und Sinneszellen eingestreut sind. Sie scheiden eine zarte (beim Regenwurm ca. 1 µm dicke), oft irisierende Cuticula ab. Innen an die Epidermis schließt sich der aus schräg gestreiften Muskelzellen bestehende Muskelschlauch an, der sich aus einer äußeren Ring- und einer inneren, viel mächtigeren Längsmuskellage zusammensetzt“ (Quelle).

Die Ursache des Irisierens

Es ist eine naheliegende Annahme, dass die Collagenstränge in der Cuticula genau wie in der obigen Skizze angeordnet sind und ein sehr feines Netz bilden. Dieses Netz erlaubt dem Wurm, sich zu strecken oder zu verkürzen, wobei sich seine Dicke ändert, ohne dass die Collagenstränge gedehnt werden. Da das Collagen einen anderen Brechungsindex hat als die feuchte Materie zwischen den Strängen, vielleicht auch weil durch die Stränge eine leicht wellige Struktur der Oberfläche entsteht, wirkt dies wie ein um den Wurm herumgewickeltes Beugungsgitter aus sich annähernd rechtwinkelig kreuzenden Linien. (Dass periodische Änderungen im Brechungsindex wie Beugungsgitter farbige Reflexe erzeugen können, wurde hier früher schon gezeigt.)

Aus der Lage der Reflexe lässt sich auch die Größe der Gitterkonstanten bzw. des Abstands benachbarter Stränge gewinnen: der Beugungsreflex erster Ordnung tritt auf, wenn der Gangunterschied der Reflexe auf benachbarten Linien gleich der Wellenlänge λ ist. Aber diesen zu berechnen ist gar nicht so einfach, daher begnüge ich mich mit einer groben Abschätzung. Ich betrachte eine bestimmte Wellenlänge, λ = 500 nm (bläuliches Grün) und lasse den entsprechenden Reflex an der Stelle auftreten, die in der benachbarten Skizze durch einen grünen Klecks markiert ist. Die Abschätzung ergibt für den Abstand der Linien voneinander etwas weniger als 500 nm.

Beugung an einem Kreuzgitter

Das Foto rechts zeigt die Beugung von Licht an einem annähernd quadratischen, sehr viel gröberen Kreuzgitter (Vorhang). Kann man am Wurm noch weitere Reflexe erwarten? Die bis jetzt beschriebenen entsprechen den Beugungsbildern erster Ordnung links, rechts, oberhalb und unterhalb des direkten Reflexes. Die weiter entfernte zweite Ordnung wird wegen der Feinheit des Gitters nicht zu sehen sein. Aber die in den Diagonalen liegenden Reflexe?

Um die Erklärung zu überprüfen, hat Aleksandr noch ein paar mehr Aufnahmen gemacht. Um das Schillern zu sehen, musste er einen Wurm in die richtige Position bringen.

Man beachte im linken Bild den Reflex links auf der Oberseite des Wurms, im rechten Bild den Reflex rechts an der Seite nahe dem unteren Bildrand. Es passt also alles zusammen.

Dünnschicht-Interferenzfarben

Es sind aber noch weitere Farberscheinungen möglich, wie das folgende Bild zeigt. Hier ist nicht die Beugung die Ursache, sondern, ähnlich wie bei einem Ölfilm auf nasser Straße, die dünne Cuticula, deren Brechungsindex sich von dem der darunterliegenden Epidermis etwas unterscheidet.

Welcher Wurm?

Die letzten Fotos zeigen übrigens, dass es sich bei den betrachteten Würmern nicht, wie zunächst vermutet, um den Gemeinen Regenwurm Lumbricus terrestris handelt, denn sie zeigen ein Merkmal, das dieser nicht hat, zahlreiche regelmäßig angeordnete winzige Borsten entlang eines Ringes um die Mitte jedes Segments. Es könnte eine Art aus den Gattungen Amynthas oder Metaphire sein, ursprünglich asiatische Regenwürmer, die in Nordamerika (woher die Fotos stammen) invasiv sind. Falls sie irisieren, dürfte dies aber bei allen Wenigborstern auf die gleiche Weise zustandekommen. Ich habe es bisher nur bei Lumbricus terrestris beobachten können.

Beugung und Interferenz an behauchter Fensterscheibe

Nach der ersten Beobachtung von Beugung am Tau auf einer Fensterscheibe habe ich dies nicht wieder gesehen. Aber haucht man eine Scheibe an, so kann man ganz ähnliche Beugungsaureolen erhalten. Wie letztens geschrieben, geht das im Sommer, wenn es warm ist, nicht so gut wie im Winter, und so habe ich im letzten Winter noch einmal ein paar Fotos von Hauchaureolen aufgenommen.

Das ging so vor sich: die Kamera wurde mit einem kleinen Stativ auf das Fensterbrett gestellt und manuell auf die entfernte Straßenlampe fokussiert. Durch eine Papierrolle wurde die Scheibe dann an der Kamera vorbei behaucht und dann mit zwei Sekunden Verzögerung (um Verwackeln zu vermeiden) fotografiert. Dann wieder behaucht und der Zyklus noch ein paarmal wiederholt. Das Ergebnis ist unten zu sehen, darunter zum Vergleich die Ergebnisse eines Versuches, das rechnerisch nachzuahmen.

Die Breite aller Bilder (Fotos und Simulationen) entspricht einem Winkel von 16°.

Der Simulationsversuch

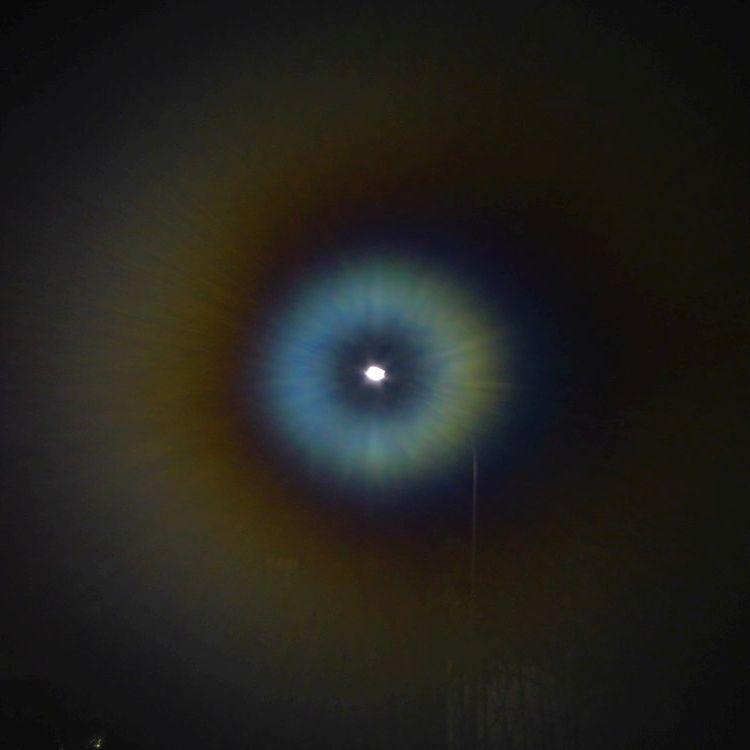
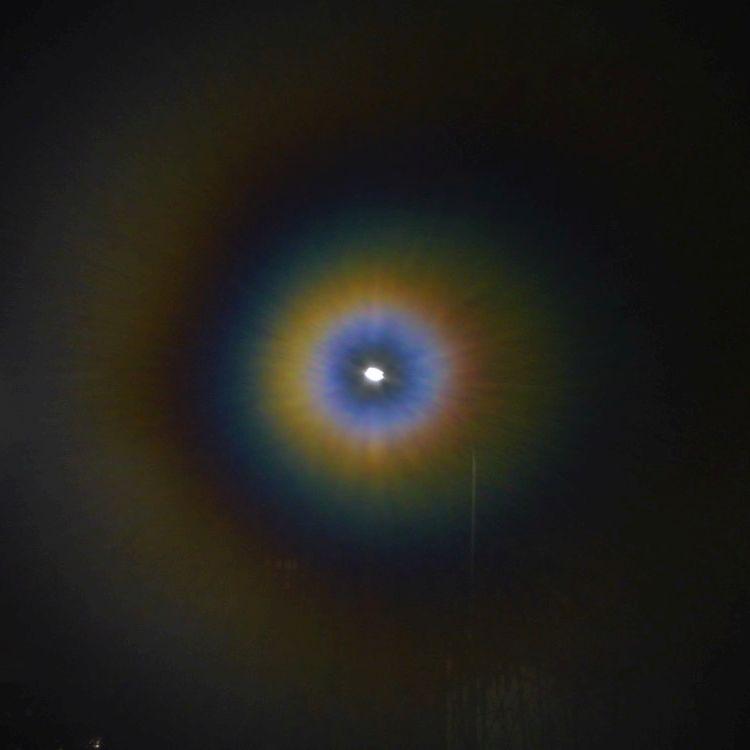
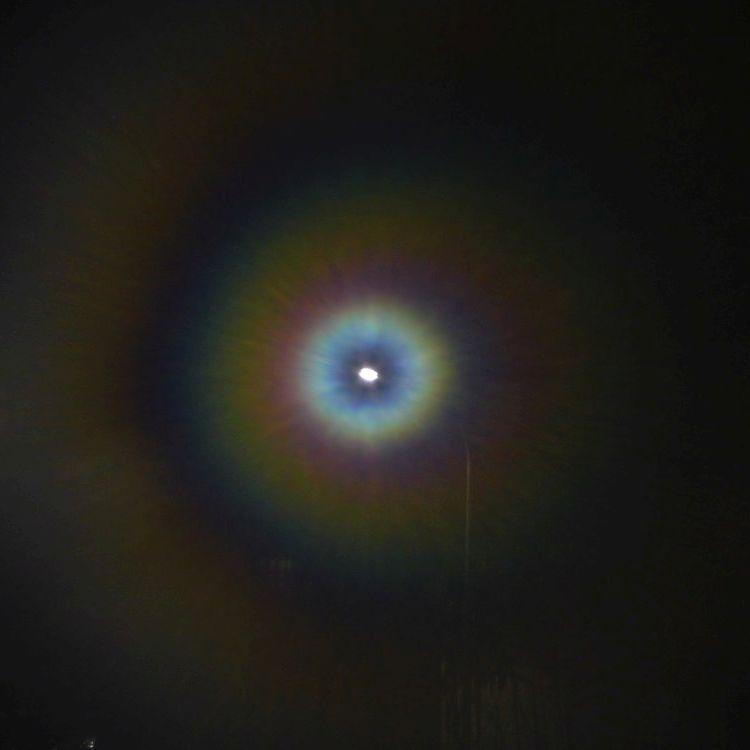
Wird eine Glasscheibe nur ganz zart angehaucht, so ist zu erwarten, dass die Verteilung der kleinen Tröpfchen einigermaßen gleichmäßig ist, denn wo gerade ein Tröpfchen kondensiert ist, ist die Dampfdichte geringer und Kondensationswärme frei geworden, so dass die Wahrscheinlichkeit, dass ein zweites Tröpfchen ganz in der Nähe kondensiert, klein ist. Man kann einen gewissen Mindestabstand zwischen den Tröpfchen annehmen.

Bei weiterer Anhauchen vergrößern sich die Tröpfchen, und wenn sich zwei berühren, fließen sie zusammen. Wahrscheinlich ziehen sie sich dann nicht auf einen genau kreisförmigen Bereich zusammen. Bei stärkerer Betauung ist somit sicherlich ein Gemisch von verschieden großen Tröpfchen vorhanden, deren Ausrichtung, falls sie länglich sind, zufällig ist. Das alles ist schwer zu berücksichtigen, hier wird daher nur ein stark vereinfachtes Modell untersucht: Tröpfchen mit kreisförmigem Umriß, deren Größe mit der Stärke der Betauung zunimmt, die statistisch verteilt sind und sich nicht berühren.

In einem ersten Versuch, die seltsamen Aureolen zu verstehen, habe ich die Tautröpfchen als undurchsichtige, also schwarze Kreisscheibchen behandelt. Ändert man in diesem Modell die Größe der Scheibchen, so verändert sich die Winkelausdehnung der Aureole, aber die Farben und ihre Reihenfolge ändern sich nicht. Diese Näherung ist, wie sich jetzt herausstellt, nur für sehr kleine Tröpfchen gut, für größere darf man ihre Durchsichtigkeit doch nicht vernachlässigen. Um die Rechnung einfach zu halten, werden statt der Hauchtröpfchen winzige fiktive, unendlich dünne Linsen betrachtet, deren Einfluss durch eine ortsabhängige Phasenverschiebung der einfallenden ebenen Wellen im Bereich der Linse berücksichtigt wird.

Berechnet wurde fraunhofersche Beugung an einem kleinen, behauchten Kreisscheibchen, dessen Durchmesser so gewählt wurde, dass jeweils ca. 500 Tröpfchen Platz fanden. Deren Verteilung wurde von einem Zufallsgenerator bestimmt, mit der Nebenbedingung eines vorgegebenen Mindestabstandes. Eine punktförmige Lichtquelle in großer Entfernung wurde vorausgesetzt mit dem Spektrum eines schwarzen Körpers mit T = 5604 K. Durch Variation der Parameter (Radius, Höhe, Mindestabstand) wurde versucht, die Bilder in der oberen Reihe nachzuahmen.

Zweifellos zeigen sich gewisse Ähnlichkeiten zwischen den beiden Reihen, aber auch deutliche Unterschiede. Einige davon lassen sich einfach erklären:

Die deutlichen radialen Streifen rühren daher, dass die Anzahl der für die Rechnung verwendeten Tröpfchen viel kleiner ist als die, die in den Fotos erfasst sind. Bei der eingestellten Brennweite von 17.5 mm und Blende f/5 beträgt der Durchmesser der Blendenöffnung 3.5 mm. Da die Kamera nahe an der Fensterscheibe und die Lichtquelle weit entfernt war, ist der erfasste Bereiches durch die Größe der Blendenöffnung gegeben. Der maximale Durchmesser des in den Simulationen verwendeten Kreisbereiches beträgt 0.9 mm (letzes Bild, da ist der Tröpfchenradius 13 μm). Außerdem ist die Lampe keine punktförmige Lichtquelle, auch das führt auf ein Verwischen etwaiger Details.

Dass das Spektrum der Straßenlampe sich stark von dem eines Schwarzen Körpers unterscheidet, das bei den Rechnungen angenommen wurde, dürfte unerheblich sein.

Beim ersten Bild in der unteren Reihe die Übereinstimmung mit dem darüber stehenden Foto sehr gut. Die Tröpfchen sind hier sehr klein (Durchmesser ca. 4 μm, also vier tausendstel Millimeter), ihre (fiktive) Höhe ist 0.6 μm und es wurde ein Mindestabstand von 6 μm (Mitte zu Mitte) angenommen. Diese kleinen Linsen haben eine sehr kurze Brennweite, zerstreuen das Licht also sehr stark und das führt dazu, dass von dort nur sehr wenig Licht zum Beobachter kommt. (Daher führt in diesem Fall die Näherung, mit schwarzen Scheibchen zu rechnen, auch schon zu guten Ergebnissen.)

Das zweite Bild in der oberen Reihe zeigt am deutlichsten, dass die Fensterscheibe ungleichmäßig behaucht wurde, daher wurden für die linke und die rechte Hälfte getrennte Anpassungen versucht, die in den Halbbildern darunter zu sehen sind.

Es zeigt sich, dass die Simulation aufgrund der idealisierenden Vereinfachungen buntere und kontrastreichere Bilder liefert als die Wirklichkeit, die Farben ändern sich in radialer Richtung in feineren Abstufungen.

Zusammenfassend lässt sich sagen, dass die überraschenden Farbwechsel der Aureole durch Interferenz des durch die Tröpfchen gehenden mit dem daneben vorbeigehenden Licht zustandekommen; der dunkle Bereich um den hellen Mittelpunkt ist eine Folge der kurzreichweitigen Korrelationen zwischen den Tröpfchen, wie anlässlich der ersten Beobachtung der Tau-Aureole schon erklärt wurde.

Fluoreszierende Bananen

Erst im Jahr 2008 wurde entdeckt, dass reife Bananen blau fluoreszieren (Bernhard Kräutler et al.: Die blaue Lumineszenz reifender Bananen - Angewandte Chemie Vol. 120, No. 46 (2008) S. 9087). Ursache der Fluoreszenz sei ein Abbauprodukt des Chlorophylls, das nur langsam zerfällt ( "Fluorescent chlorophyll catabolites ..."). Siehe auch Chemistry in Pictures: Blue bananas.

Aufnahmen unter Tageslicht und unter Schwarzlicht. (Schwarzlicht ist Ultraviolettstrahlung mit Wellenlänge um 366 nm laut Herstellerangabe der Lampen.)

Lässt man die Bananen länger liegen, so entstehen auf der Schale braune Flecken durch den Zerfall von Zellen. Um diese herum ist die Fluoreszenz besonders hell.

Seltsam finde ich, dass das Wissen, dass sie gelb sind, dazu führt, dass man beim Betrachten der blau fluoreszierenden Bananen – zumindest mir geht es so – meint, ein etwas gelbliches Blau zu sehen, das es ja nicht geben kann. Das kommt vielleicht auch durch den Kontrast zu den heller fluoreszierenden Ringen zustande.

Lässt man die Bananen noch länger liegen, so vergehen die hellen fluoreszierenden Ringe und das Leuchten lässt insgesamt wieder nach und verschwindet schließlich völlig. Überraschenderweise fluoresziert aber die helle Innenseite der Schale noch weiterhin, selbst wenn die Schale schon vertrocknet ist.

Regenbogenfarben

Bei wechselhaftem Herbstwetter mit gelegentlichen Regenschauern gab es öfters schöne Regenbögen in kräftigen Farben.

Man meint fast, alle Spektralfarben zu sehen – Rot, Orange, Gelb, Grün, Blau und Violett, allerdings Blau und Violett schon sehr „verdünnt“. Um das besser beurteilen zu können, wird das Foto mit einer grauen Maske abgedeckt, die nur einige Stellen freilässt. Zunächst aber erst noch die Positionen der freigelassenen Stellen:

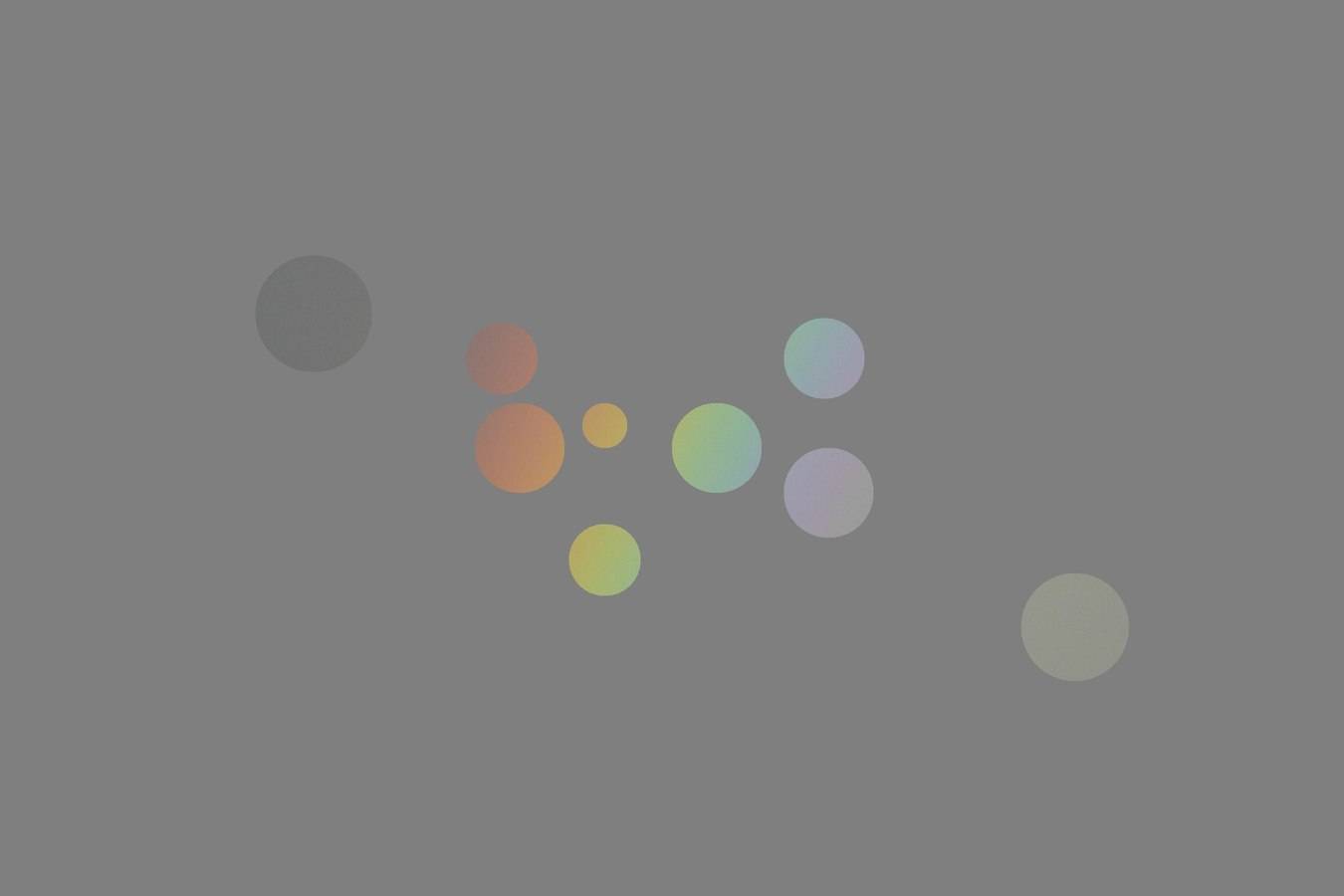
Selbst das kräftige Rot am äußeren Rand des Bogens erscheint hier in neutraler Umgebung nicht mehr so kräftig. Und wenn statt Grau eine schwarze Umgebung gewählt wird, sieht man noch besser, wie gering die Farbsättigung in allen Fällen ist:

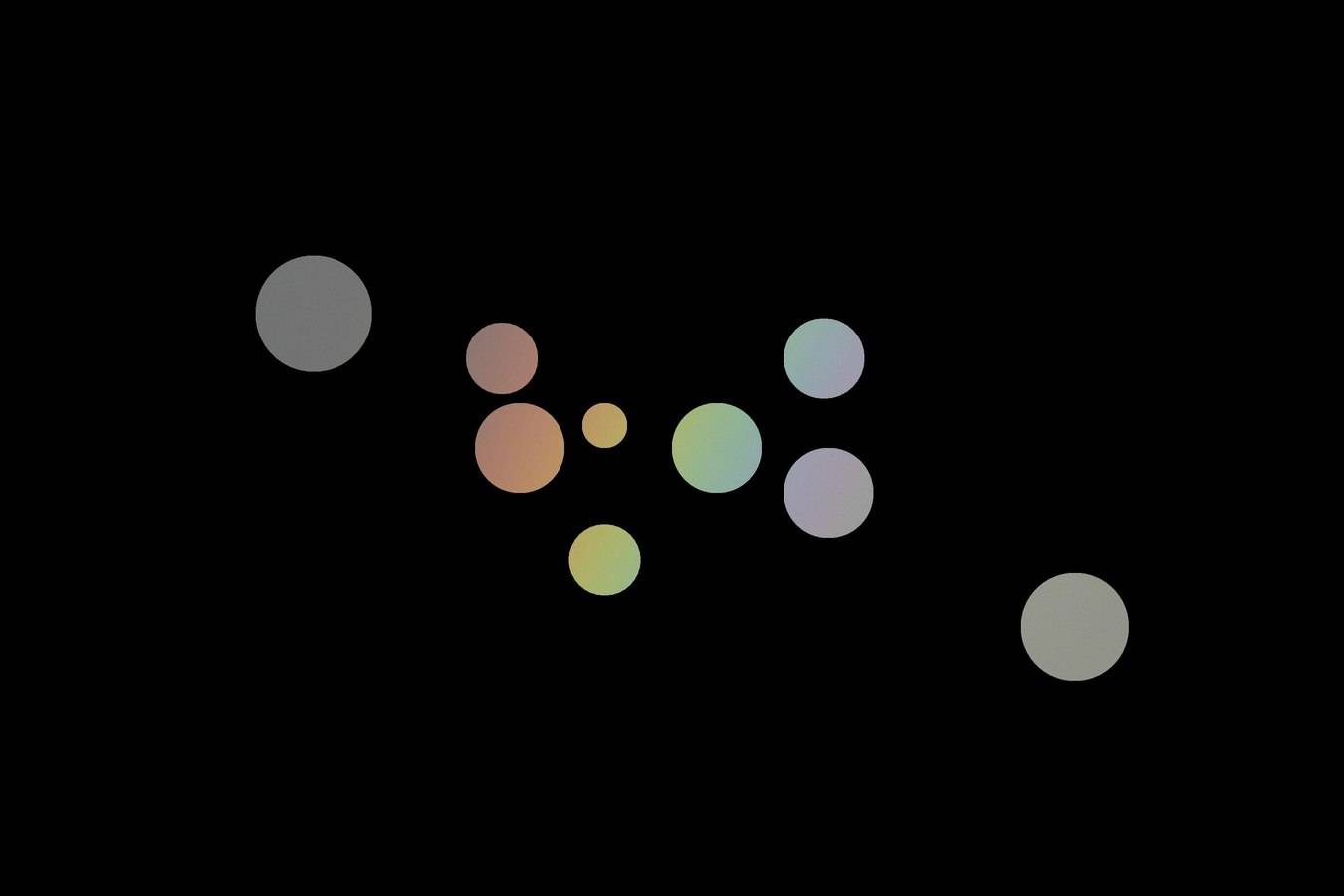
Vor einem hellgrauen oder weißen Hintergrund sieht man die Farben wieder anders, das Rot ist nun braun, das Gelb olivgrün, das Violett ist kaum mehr zu erahnen:

Hier wird deutlich, wie veränderlich die Farbempfindungen sind und wie stark sie durch Kontraste mitbestimmt werden.

Doppelbrechung und Polarisation, Komplementärfarben

Ein Kästchen aus Kunstharz reflektiert das Licht vom bedeckten Himmel, und man sieht, wegen der inneren Spannungen und der dadurch hervorgerufenen Doppelbrechung, ganz schwache Farben.

Bei schrägem Lichteinfall ist das von einer glatten Oberfläche eines transparenten Körpers reflektierte Licht teilweise polarisiert. Falls der reflektierte und der gebrochene Strahl senkrecht aufeinander stehen, sogar zu hundert Prozent; den entsprechenden Einfallswinkel nennt man Brewster-Winkel. Dann wird nur das Licht reflektiert, dessen elektrisches Feld senkrecht auf die Einfallsebene schwingt (s-Polarisation; die Einfallsebene wird von der Flächennormalen und der Strahlrichtung aufgespannt), während das in der Einfallsebene schwingende (p-Polarisation) die Grenzfläche ungeschwächt passiert.

Das an der Oberseite der Acrylglasscheibe reflektierte Licht ist polarisiert, aber davon merkt man nichts, wenn man kein Filter verwendet. Das an der Unterseite reflektierte, ebenfalls polarisierte, Licht geht nun durch das infolge der inneren Spannungen doppelbrechende Material und wird dabei in einen ordentlichen und einen außerordentlichen Strahl aufgespalten, zwischen sich denen sich eine Phasendifferenz ergibt, wie an anderer Stelle etwas ausführlicher beschrieben.

Im linken Bild ist die Durchlassrichtung des Filters vor dem Objektiv so, dass die s-Wellen blockiert werden; diese Situation entspricht also einem doppelbrechenden Medium zwischen gekreuzten Polarisatoren. Ohne Doppelbrechung wäre die ganze Fläche nahezu schwarz.

Im rechten Bild ist die Filterstellung gegenüber der im linken um 90° verdreht, die s-Wellen werden durchgelassen und die p-Wellen blockiert. Ohne Doppelbrechung wäre die Fläche einheitlich weiß.

Dass ohne nachgeschaltetes Polarisationsfilter auch schon Farben zu sehen sind, wenn auch nur schwach, kommt daher, dass beim Durchgang des von unten reflektierten Lichtes durch die obere Grenzfläche die p-Wellen kaum geschwächt werden, während ein nennenswerter Teil der s-Wellen wieder reflektiert wird und daher im transmittierten Licht fehlt.

Elliptische Polarisation, Zirkularpolarisation

In einem doppelbrechenden Medium wird aus linear polarisiertem Licht im allgemeinen elliptisch polarisiertes. Dieses kann man als Überlagerung von zwei aufeinander senkrecht linear polarisierten Wellenzügen auffassen oder aber auch als Überlagerung von rechtszirkular und linkszirkular polarisierten Wellen verschiedener Amplitude. Mit Zirkularpolarisationsfiltern, wie sie in Brillen für 3d-Filme verwendet werden, kann man diese Anteile getrennt zeigen:

Das linke Bild ist durch das linke Brillenglas einer „3-d-Brille“ aufgenommen, man sieht also das linkszirkular polarisierte Licht, das rechte entsprechend durch das rechte Glas aufgenommene zeigt den rechtszirkularen Anteil.

Die additive Überlagerung der beiden Bilder müsste eigentlich so aussehen wie das erste Bild ganz oben. Das heißt, die im linken und rechten Bild an einander entsprechenden Stellen gesehenen Farben sind annähernd komplementär. Annähernd, weil das oberste Bild ja schwache Farben zeigt, aber dazu kommt noch, dass die Aufnahmen freihändig gemacht wurden und der Blickwinkel daher links und rechts nicht exakt der gleiche ist. (Darüber hinaus funktioniert die Analyse der Zirkularpolarisation durch ein Filter exakt nur für eine einzige Wellenlänge, aber wie sich das genau auswirkt, soll hier nicht untersucht werden.)

Lokale Adaptation, Nachbilder

An den fließend ineinander übergehenden Farben kann man gut eine Besonderheit unseres Gesichtssinnes testen. Dazu wurde im nächsten Bild ein Fixationspunkt in der Mitte durch ein + markiert. Wenn man länger auf diesen Punkt starrt, so verblassen die Farben und verschwinden nach ca. 30 Sekunden ganz. Das geht schneller, wenn man nur mit einem Auge schaut. Dass beim Fixieren eines Punktes Teile aus dem Gesichtsfeld verschwinden, wurde zuerst von dem Schweizer Arzt I.P.V. Troxler beschrieben, daher der Name Troxler-Effekt. Er kommt durch die gleichen „Mechanismen“ zustande, die Nachbilder erzeugen. Kontinuierliche Übergänge zwischen den verschiedenen Bereichen reduzieren die Wirkung unbeabsichtigter Augenbewegungen, die sonst den Effekt verzögern oder verhindern.

Wenn Sie anschließend auf eine weiße Fläche schauen (aufs Bild klicken!), sehen Sie für kurze Zeit als Nachbild das Negativ. Interessant finde ich auch, wie sich das Nachbild verändert: zuerst verschwinden die Farben, der Helligkeitsunterschied baut sich langsamer auf und klingt viel langsamer ab.

Beugungsmuster am Fliegenauge

Aleksandr Berdnikov gelang diese Aufnahme des fresnelschen Beugungsmusters auf den Facettenaugen einer Fliege. Ich habe früher schon ähnliche Muster auf Libellenaugen gezeigt, aber auf diesem Bild sind die einzelnen Facetten deutlich zu sehen.

„Meine Erklärung dafür ist, dass (vereinfachend) jede einzelne Facette des Auges ein sphärischer Spiegel ist, der eine punktförmige Lichtquelle – das Bild der Sonne – etwas unterhalb der Kappe erzeugt. Das reflektierte Sonnenlicht ist also im Grunde so, als ob es von diesem Punkt ausgehend durch die sechseckige Öffnung der Facettenkappe hindurchginge: es breitet sich in einem sechskantigen Kegel aus und zeigt in der Nähe, na ja, der Ränder ein Beugungsmuster.

Und wir sehen diese Intensitätsverteilung auf das Auge «abgebildet», da die Richtung der Reflexionskegel der Ausrichtung der Facetten folgt, so dass eine (nicht so) weit entfernte Kamera auf jeder Facette den entsprechenden Punkt des Kegels erfasst.“

Der Öffnungswinkel der reflektierten Lichtkegel ist viel größer als bei den früher gezeigten Libellenaugen, die Beugungsmaxima und Minima sind nur an den Rändern zu sehen und entsprechen denen, die an Rändern von allen Schatten auftreten müssten, wenn die Lichtquelle punktförmig wäre. Die Winkelausdehnung der Sonnenscheibe ist jedoch so groß, dass sich diese Erscheinungen im Halbschattenbereich herausmitteln.

Das Negativ

Heute, wo überwiegend digital fotografiert wird, hat das Negativ an Bedeutung verloren. Gängige Bildbearbeitungsprogramme bieten jedoch die Möglichkeit, ein Bild in sein Negativ umzuwandeln. Das Ergebnis sieht meist recht plausibel aus. Hier ein Beispiel:

Der Anlass, das zu untersuchen, ergab sich bei der Demonstration von Versuchen mit einem Prisma. Betrachtet man einen weißen Streifen auf schwarzem Grund und einen schwarzen Streifen auf weißem Grund, so sollten sich die beiden Bilder zueinander doch wie Positiv und Negativ verhalten oder, anders ausgedrückt, an einander entsprechenden Stellen sollten jeweils die Komplementärfarben zu sehen sein.

Das erste Bild in der Reihe unten zeigt die Vorlage, das zweite diese durch ein Prisma fotografiert. Dazu ist zu sagen, dass die Farben, die man sieht, wenn man den schmalen weißen Streifen durchs Prisma anschaut, alle außerhalb des auf dem Bildschirm darstellbaren Bereiches liegen. Dagegen sind alle Farben, in denen man den schwarzen Streifen auf weißem Grund sieht, exakt reproduzierbar. Das zweite Bild kann daher in der rechten Hälfte nur ungefähr wiedergeben, was zu sehen ist. Das vierte Bild ist durch Umwandlung des zweiten mit einem Bildbearbeitungsprogramm in ein „Negativ“ entstanden – es sollte eigentlich wie ein Spiegelbild des zweiten aussehen.

In den Bildern werden die Helligkeiten von R, G und B für die Darstellung auf dem Bildschirm durch Zahlen L von 0 bis 255 angegeben. Ersetzt man L jeweils durch 255 − L, so erhält man die umgedrehten Farben im vierten Bild. So wird die Umkehrung durch die Bildbearbeitungsprogramme durchgeführt.

Um ein richtiges Negativ zu erhalten, dürfen nicht die empfundenen Helligkeiten invertiert werden, sondern die physikalischen Intensitäten Y, die nichtlinear über die sogenannte Gamma-Korrektur mit der Helligkeit zusammenhängen. Diese Rechnung wurde durchgeführt, um das dritte Bild in der obigen Reihe zu bekommen. Tja, es sieht auch nicht genau so aus, wie das Spiegelbild des zweiten, aber es ist diesem immerhin ähnlicher. Der Grund für die Diskrepanz ist, dass die exakten Farben nicht dargestellt werden können, und für die in den darstellbaren Bereich projizierten gilt nicht mehr, dass die linke Bildhälfte das Negativ der rechten ist und die exakten Komplementärfarben zeigt.

Panorama mit Mond

Die beleuchtete Seite des Mondes zeigt zur Sonne – aber warum sieht es so aus, als ob sie etwas weiter nach oben zeige, wenn die Sonne tief steht oder gar schon untergegangen ist?

Für ein Panoramabild ist die Erklärung ganz einfach. Das dreidimensionale Bild wird auf einen Zylindermantel projiziert und dieser wird dann ausgebreitet. Geraden werden dadurch im allgemeinen auf gekrümmte Linien abgebildet.

Aus zwei Bildern mittels AutoStitch zusammengesetztes Panorama. Nahe der linken oberen Ecke ist der Mond zu sehen, rechts zwischen den Hausdächern die Sonne.

Da der Mond suf dem Bild nur so winzig klein ist, links ein Ausschnitt aus dem Foto in Originalgröße, an dem man die Richtung besser sehen kann.

Wenn Mond und Sonne beide am Himmel stehen, entspricht das, was man wahrnimmt, überraschenderweise(?) dem Panoramabild, der Mond scheint von weiter oben und nicht von der Sonne beleuchtet. Dazu schreibt Minnaert (1937) [1]

Die Linie, die die „Hörner“ der Mondsichel verbindet, scheint keineswegs senkrecht auf die Richtung von der Sonne zum Mond zu stehen. Aber wenn man diese Richtung durch einen gespannten Faden fixiert, den man so hält, dass man das eine Ende vor der Sonne sieht, das andere vor dem Mond, so unwahrscheinlich das zunächst scheint – die beiden Linien bilden einen rechten Winkel. (Frei übersetzt aus [2].)

Die Erklärung ist im Grunde ganz einfach. Wenn wir den Mond ansehen, können wir uns leicht eine gerade Linie vorstellen, die in der Richtung der auf den Mond einfallenden Strahlen verläuft. Wenn wir dann den Kopf drehen und in Richtung Sonne schauen, gelingt es uns nicht, diese gedachte Linie wiederzufinden und richtig bis zu ihrem Fluchtpunkt in der Sonne fortzusetzen, so lange wir keine zusätzlichen Hilfen wie den erwähnten gespannten Faden haben.

Wenn wir den Faden sehen, während wir den Kopf drehen, verändert sich sein Bild auf der Netzhaut im Auge. Diese Veränderung wird kaum bemerkt, denn wir nehmen nicht die Bilder auf der Netzhaut wahr, sondern sehen, was draußen ist; hier, dass der Faden gerade ist und seine Lage beibehält. Das räumliche Sehen erfordert einen immensen Aufwand an Datenverarbeitung, der uns kaum je bewusst wird. Und bei einer nur gedachten geraden Linie fehlt die nötige Information, um die unmerklichen Veränderungen zu berücksichtigen.

Es gibt allerdings noch einen Trick, diesen Mangel zu umgehen: wenn die Drehung des Kopfes beim Blickwechsel um eine Achse senkrecht auf die Ebene erfolgt, die die Sonne, den Mond und das Auge enthält, dann ändert sich das Bild der gedachten Linie auf der Netzhaut nicht, und die fortgesetzte Gerade trifft die Sonne [3].

[2] M. Minnaert "The nature of LIGHT & COLOR in the open air", Dover Publications Inc., New York 1954, ISBN 0800759201969; p. 152

[3] U. Backhaus und H.J. Schlichting, "Der Silberblick des Mondes" MNU Journal 4.2017

Abendrot, Himmelsfarben

Weißabgleich

Die Farbe des Himmels durch Fotos zu dokumentieren ist nicht einfach, und das gilt besonders bei Dämmerung und Dunkelheit. Das liegt daran, dass sich die Beleuchtung im Tagesverlauf stark ändert und dass sich unser Farbempfinden auf diesen Wechsel einstellt (Farbumstimmung). Damit Fotos natürlich wirken, soll dieser Farbumstimmung Rechnung getragen werden; dies geschieht durch den Weißabgleich. Eine neutralgraue Fläche soll auch auf dem Foto neutralgrau erscheinen, so wie wir sie eben wahrnehmen. Die Farbe der Beleuchtung wird durch den Weißabgleich gewissermaßen herausgerechnet, die Szenerie soll so aussehen, wie sie bei „normalen Tageslicht“ aussähe. Als Tageslicht-Weiß gilt die Beleuchtung D65, annähernd die Farbtemperatur von 6504 K.

Wenn man aber die Farbe der Beleuchtung selbst, in diesem Fall also des Himmels, auf dem Foto sehen will, dürfte man eigentlich keinen Weißabgleich durchführen, sondern müsste D65 als Weiß festlegen. Nur – stimmt das Ergebnis dann mit der Empfindung überein?

Fotos vom 18. Dezember 2019, eine halbe Stunde nach Sonnenuntergang. Die Bilder lassen sich durch Anklicken vergrößern!

Das linke und das mittlere Bild zeigen dasselbe Foto. Links mit Weißabgleich auf 6500 K, in der Mitte auf 10000 K. Wenn auch das linke Bild die Farben am getreuesten wiedergibt, entspricht doch das mittlere besser dem optischen Eindruck. Über dem Rot in Horizontnähe habe ich den Himmel eher grau als blau gesehen.

Bei Einstellung auf 9000 K und einer leichten Verschiebung auf der Rot-Grün-Achse in Richtung Grün ergeben sich die Farben so wie im rechten Bild, dieses wurde aber mit derselben Kamera und mit der gleichen Einstellung wie das große Bild oben aufgenommen. Es kommt dem subjektiven Empfinden auch sehr nahe.

Die einfache Kamera, die ich 2006 für das Foto vom Abendrot verwendete, bot nicht die Möglichkeit, das Rohformat abzuspeichern. Der Weißabgleich war auf „bewölkt“ eingestellt und soweit ich das damals beurteilt habe, war die Farbwiedergabe sehr gut.

JPEG-Kompression

Der Sachverhalt, dass wir Helligkeitsunterschiede viel deutlicher empfinden als Farbtonunterschiede bei gleicher Helligkeit, wird bei der JPEG-Kompression eines Bildes ausgenutzt, indem die Farb-Information mit geringerer Auflösung gespeichert wird als die der Helligkeit. Dazu werden die gemessenen Werte R, G und B für jedes Pixel in Helligkeit und die zwei Farbkanäle „Blau—Gelb“ und „Rot—Grün“ umgerechnet. Auf Details soll hier nicht eingegangen werden.

Der Verlust an Information fällt bei Fotografien nur selten auf, aber im ersten Bild oben kann man bei genauem Hinsehen bemerken, dass die Farbe des Himmels an vielen Stellen nicht bis an die dunklen Äste heranreicht. Rechts ist ein Bildausschnitt in Originalgröße wiedergegeben, durch Draufklicken kann man ihn auf zwei zu eins vergrößern.

Die Physik zu Himmelsblau und Abendrot finden Sie in dem Abschnitt über Streuung.

Eisblumen

Tagsüber, am 10. November, war das Wetter trüb und feucht gewesen, doch am Abend klarte es auf. In der Nacht bemerkte ich, dass sich an einem schrägen Dachfenster außen Eisblumen gebildet hatten. Die Straßenlampe gegenüber beleuchtete das Fenster und die schon kahlen Zweige des Baumes vor dem Haus warfen ihre Schatten darauf.

Vor Jahren hatte ich schon einmal ähnliche Eisblumen gesehen [1], und auch dieses Mal zeigte sich das seltsame, sich annähernd periodisch wiederholende Glitzern entlang der Mittellinien der einzelnen Bänder.

Die Blätter zeigen nicht die gleiche fiederige Struktur wie die zuletzt beschriebenen, vermutlich weil der Wasserfilm auf dem Fenster dieses Mal etwas dicker war. Statt Fiederchen sieht man hier eine scheinbar dreidimensionale Struktur, wie ein Gewirr von sich nach unten verzweigenden Wurzeln. Der Abstand zwischen den glitzernden Stellen betrug sechs bis sieben Millimeter. Als Erklärung der annähernd periondischen Wiederholungen der Strukturen kann ich anbieten, was ich im Wesentlichen letztens schon geschrieben habe:

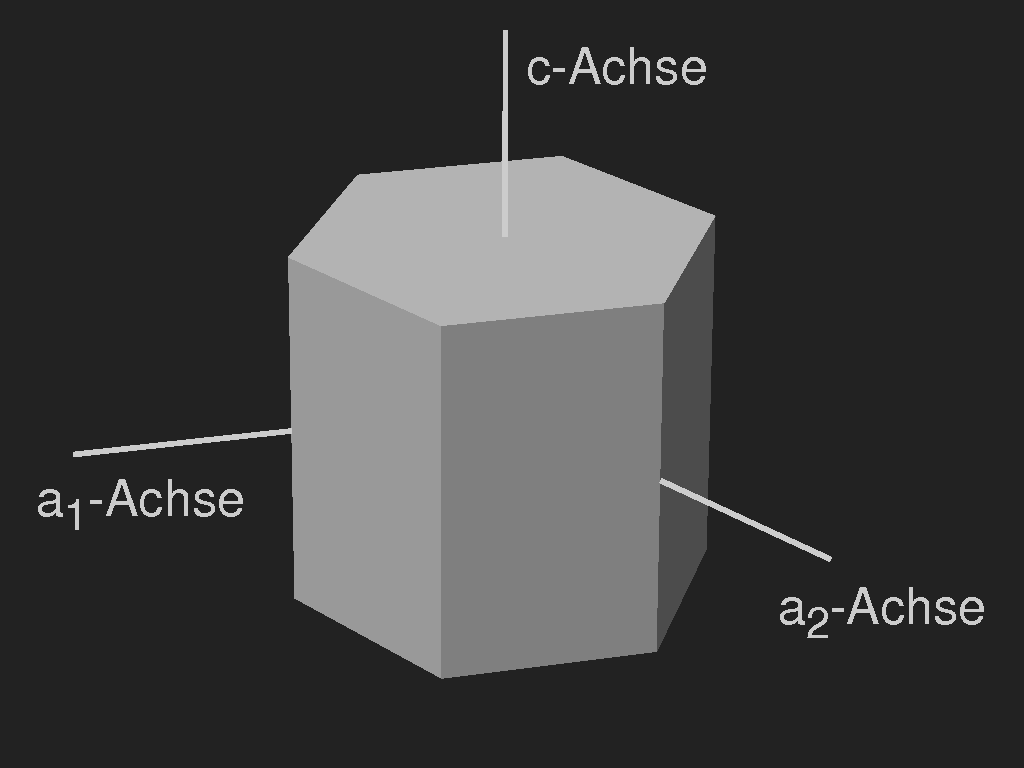
Das Wachstum geschieht durch Anlagerung von Molekülen, dabei wird Wärme frei, die, wenn sie nicht abgeführt wird, das weitere Wachstum hemmt. Sowohl für die Anlagerung als auch die Wärmeabfuhr sind die äußeren Ecken bevorzugt. Die dendritischen Schneekristalle sind wohlbekannt, aber es kommen seltener auch flache bis stäbchenförmige Prismen mit sechseckiger Grundfläche vor.

Die Krümmung der einzelnen Dendriten wird wahrscheinlich durch Temperaturunterschiede (Gradienten) verursacht, die infolge der ungleichmäßigen Ausdehnung des Kristallgitters die Bildung von Gitterfehlern begünstigen, wodurch sich die Orientierung des Kristallgitters bei fortschreitendem Wachstum langsam ändert. Angenommen, die c-Achse liegt parallel zur Glasoberfläche und das dendritische Wachstum erfolgt vorzugsweise in Richtung der a-Achsen wie bei den sternförmigen Schneekristallen. Das Kristallgitter kann sich nach den Seiten, aber auch nach oben oder unten krümmen, während die Dendriten an die Oberfläche gebunden sind, da sie nicht aus dem Wasserfilm herauswachsen können. An der Oberseite bilden sie Facetten aus, deren Ausrichtung durch das Kristallgitter bestimmt wird und sich somit langsam ändert. Das Periodizitätsintervall entspricht einer Drehung des Gitters um 60°. Dies wird durch das folgende Bild schematisch illustriert.

Die Änderung der Orientierung der oberflächlichen Facetten bewirkt sowohl das periodische Auftreten der hellen Stellen entlang der Blattachsen als auch die Helligkeitsunterschiede quer zu den Achsen, wodurch der Eindruck von räumlicher Tiefe hervorgerufen wird.

Schilfrohr

Herbst, die Sonne steht schon tief, und am Weg entlang des Wassers steht Schilfrohr (Phragmites australis). An den Rispen mit den in Ährchen reifenden Samen glänzen im Sonnenlicht die Haare, die für die Verbreitung der Samen durch den Wind sorgen, und im Gegenlicht lassen sich verschiedene optische Erscheinungen beobachten.

Lichtringe

Interferenzfarben

Im nächsten Bild kann man den Glanz der dünnen Härchen in zarten Farben sehen. Die Farben kommen zustande, wenn die Lichtstrahlen, die von nahe benachbarten Stellen einen Punkt auf dem Sensor des Fotoapparates erreichen, sich in der zurückgelegten Wegstrecke ein wenig unterscheiden, überlagern, wobei durch Interferenz Teile des Spektrums abgeschwächt oder ausgelöscht, andere verstärkt werden. Solche Interferenzfarben im Gegenlicht vor dunklerem Hintergrund zeigen sich an vielerlei fädigen Strukturen, Distel-Samenhaaren [2], Raupengespinsten [3] und besonders deutlich an Spinnwebfäden [4]. Diese Farben sind mit freiem Auge nicht so gut zu sehen, denn sie sind am deutlichsten, wenn sich die Fäden etwas außerhalb des Schärfebereiches befinden, und beim Hinsehen fokussiert man ja unwillkürlich.

Fresnelsche Beugung

Ob und wie deutlich Effekte der Fresnelschen Beugung auf den Fotos sichtbar werden, hängt von den Parametern der Kamera ab; die Beugung erfolgt ja an der Blendenöffnung und ist daher mit freiem Auge in dieser Form ebenfalls nicht zu sehen. Die Blendenöffnung betrug hier f/7.1, die Brennweite f = 8.4 mm und der Pixelpitch beträgt 1.5 μm.

Die Beugungseffekte zeigen sich in der Form, dass ein heller Punkt außerhalb der Schärfeebene nicht einfach verschwommen abgebildet wird, sondern ein von der Form der Blende abhängiges Muster zeigt, wie schon einmal am Beispiel von Regenbogenreflexen an Tautröpfchen [5] beschrieben. Wo die Härchen entlang von Linien glänzen, äußert sich die Beugung, dass statt einer diffusen Linie zwei oder drei durch dunklere Streifen getrennte Linien zu sehen sind, einzelne Glanzflecke zeigen eine dunkle Mitte.

Leuchtende Nachtwolken

Die folgenden Bilder wurden in Wunstorf (9.27° E, 52.25° N) aufgenommen, daraus und aus dem Aufnahmezeitpunkt wurde die Sonnenhöhe berechnet.

Die Wolken bestehen aus winzigen Eiskristallen bis ca. 100 nm Durchmesser und bilden sich in Höhen um 76 bis 85 km (engl. Wikipedia) oder 81 bis 85 km (deutsche Wikipedia). Bei Tag können diese Wolken, auch wenn sie vorhanden sind, nicht gesehen werden, sie sind sehr dünn und transparent und werden vom übrigen Himmelslicht überstrahlt. Aber wenn sie in der Nacht oder bei Dämmerung von der Sonne beleuchtet werden, während die tieferen Luftschichten im Schatten liegen, dann werden sie sichtbar.

Wiedergabetreue

Es ist nicht einfach, die Bilder so wiederzugeben, wie man sie ursprünglich gesehen hat. Das hat verschiedene Gründe. Zum Einen sieht man ja bei Dunkelheit keine Farben (skotopisches Sehen), bei Dämmerung (mesopisches Sehen) die Farben nicht so gut wie bei Tageslicht (photopisches Sehen). Und was sind dann die richtigen Farben, die man dokumentieren will? Ich habe diese Problematik im Zusammenhang mit dem Polarlicht schon einmal angesprochen. Bei Dunkelheit kann man sich auf den automatischen Weißabgleich durch die Kamera nicht verlassen. Das wird besonders deutlich, wenn, wie hier, verschiedene Lichtquellen im Spiel sind. Die Straße und das Gebüsch im Vordergrund werden von einer Straßenlampe hell erleuchtet, ein befriedigender Kompromiss mit dem Leuchten im Hintergrund ist nicht möglich.

Die Bilder wurden im Rohformat gespeichert, so dass eine nachträgliche Einstellung des Weißabgleichs möglich war. Ich habe den Nachthimmel nicht blau, sondern grau gesehen und daher die Farbtemperatur für „Weiß“ auf 6500 K gesetzt (das entspricht Tageslicht im Schatten).

Die Farben

Da die streuenden Eiskristalle klein im Vergleich mit den Wellenlängen des Lichtes sind, wird das kürzerwellige Licht stärker gestreut als das längerwellige und die Wolken erscheinen daher bläulich, so wie im Kapitel über Streuung beschrieben (Rayleigh-Streuung, Tyndall-Effekt). Je weiter entfernt die Wolken jedoch sind, desto mehr verschiebt sich der Farbton in Richtung weißlich-gelblich-rötlich, wieder aufgrund der Streuung in der Luft. Und die in größtmöglicher Höhe gesehenen Wolken sind auch nicht mehr bläulich. Die Strahlen, die sie beleuchten, haben einen langen Weg durch die unteren, dichteren Luftschichten zurückgelegt und sind daher orange bis rötlich wie das Licht der untergehenden Sonne.

Links ein Ausschnitt aus einer Aufnahme vom 3. Juli 2019, 2:59 MESZ; H = −12.19°. Rechts eine schematische, nicht maßstabstreue Skizze.

Gespiegeltes Eis

Wenn sich auf dem Wasser eine dünne Eisschicht gebildet hat, kann man bei schönem Wetter, also blauem Himmel, die durch die Doppelbrechung entstehenden Farben ohne alle Hilfsmittel beobachten. Überrascht es, dass nur die Spiegelbilder bunt sind? Die drei Aufnahmen hat Daniela Rapavá ohne Polarisationsfilter gemacht. (Mit Filter würden auch die Eisplatten selbst farbig erscheinen.)

Wie kommt es dazu? – Die Erklärung dieser Erscheinung findet sich in dem Abschnitt Polarisation und Doppelbrechung am Beispiel eines Kunststoffkästchens, und auch bei den in einem Folientunnel-Gewächshaus fotografierten Farben.

Strahlen und von unten beschienene Wolken

Die Sonne scheint durch Lücken zwischen den Wolken und in der durch Dunst oder Staub getrübten Luft sieht man die parallelen Strahlen perspektivisch wie einen Fächer. Das ist kein seltener Anblick. Bei tiefstehender Sonne können sich solche Strahlen, die dann Dämmerungsstrahlen genannt werden, über einen großen Teil des Himmels erstrecken.

Hier modellieren nicht Wolken, sondern ein Bergkamm die Dämmerungsstrahlen. Die Wolken über den im Dunst sichtbaren Strahlen werden von der untergehenden Sonne von unten beleuchtet. Auf dem nächsten Bild ist die Beleuchtung der Wolkenunterseite noch besser zu sehen.

Es sind zwar keine Dämmerungsstrahlen vorhanden, dafür aber Schatten, die von den tieferen Partien der Wolken auf die höheren Schichten geworfen werden. So deutlich zeigt sich dieses Indiz für die Kugelgestalt der Erde nur selten.

Kein Dämmerungsstrahl, sondern eine Lichtstraße auf der von unten beleuchteten Wolke. Plättchenförmige Eiskristalle in der Wolke, die sich beim Absinken horizontal ausrichten und um diese Mittellage schwanken, spiegeln die Sonne. Meist empfindet man diese Erscheinung als eine vertikale Lichtsäule (die übliche Bezeichnung), aber sie kommt auf die gleiche Art zustande wie eine Lichtstraße auf dem Wasser, nur oben und unten vertauscht.

Gekrümmte Lichtstrahlen

Windräder eines Windparks ca. 35 km nördlich von Juist, gesehen von Juist aus. (© Chris Dziat. Das Bild ist ein Screenshot aus einem Video. Wiedergabe der Bilder mit freundlicher Genehmigung.)

Mit freiem Auge waren die Windräder kaum zu sehen (Weitwinkelaufnahme, mittlere Brennweite); sie wurden „herangezoomt“. Unter der Voraussetzung gerader Lichtstrahlen und eines geraden Untergrundes wäre dieses Bild nicht möglich. Aber man sieht deutlich die Luftspiegelung nach unten, also sind die Lichtstrahlen, die dieses Spiegelbild erzeugen, gekrümmt.

Die Aufnahme wurde am 18. März 2018 gemacht; die Luftschicht unmittelber über der Wasserfläche muss etwas wärmer gewesen sein als die Schichten darüber, so dass sich die Strahlen nach oben krümmen. Die nebenstehende Skizze zeigt dies schematisch (und stark übertrieben). Unten ist die Luft wärmer, der Brechungsindex kleiner und daher die Wellenlänge größer als oben.

Die zackig-wellige Grenzlinie zwischen Himmel und Wasser ist nicht der Horizont, sondern der untere Rand des Spiegelbildes. Der Horizont ist auf der Höhe, wo sich die Rotorblätter und ihr Spiegelbild in dem abgerundeten Knick zu berühren scheinen.

Eine leichte Krümmung der Lichtstrahlen in der Atmosphäre ist immer vorhanden, da die Dichte der Luft und somit ihr Brechungsindex von der Höhe und von der Temperatur abhängt. Das macht sich vor allem bei nahezu horizontal verlaufenden Strahlen bemerkbar. Da die Dichte der Luft im Allgemeinen mit zunehmender Höhe abnimmt, sind die Strahlen gewöhnlich ganz schwach nach unten gekrümmt. Das hat zur Folge, dass die Sichtweite größer ist, als sie ohne die Lichtbrechung wäre, und man kann das berücksichtigen, indem man statt mit der Krümmung der Erdoberfläche mit einer scheinbaren Krümmung rechnet, die etwas geringer ist (größerer scheinbarer Erdradius). (Laut Wikipedia beträgt der mittlere scheinbare Erdradius R_s ≈ 7680 km.) Dies wird weiter unten noch genauer ausgeführt.

Allerdings spielt der Temperaturverlauf eine große Rolle. Wenn die Temperatur nach oben zunimmt, kann die Sichtweite stark vergrößert werden, wenn die Lichtstrahlen der Erdkrümmung folgen, und es können sogar Luftspiegelungen nach oben auftreten (Fata Morgana).

Windräder in ca. 40 km bis 60 km Entfernung nordwestlich von Juist, kurz nach Sonnenuntergang am 28. Juni 2018, aufgenommen von Juist aus aus ca. 20 m Höhe. (Screenshot aus einem Video von Chris Dziat.)

Nach der Karte der Offshore Windkraftanlagen in der Deutschen Bucht dürften diese Windräder zu dem Windpark Borkum-Riffgrund II gehören.

Das Bild entstand Ende Juni, als das Wetter sehr warm war. Das Wasser war kälter als die Luft, so dass die unteren Luftschichten vermutlich kühler waren als die etwas höheren (Inversion) und sich erst in größerer Höhe der normale Temperaturverlauf einstellte.

Terrestrische Refraktion

Glastürprisma

Die tiefstehende Herbstsonne scheint auf die gläserne Eingangstür des Niedersächsischen Landesmuseums in Hannover. Licht, das auf die abgeschrägte Kante trifft, wird in ein Prismenspektrum aufgespalten. Das ist im mittleren Bild schematisch skizziert. Rechts ist in dem vergrößerten Ausschnitt zu sehen, dass das Spektrum in größerer Entfernung vom Prisma nur die drei Farben Rot, Grün und Blau zeigt (was übrigens auch schon Goethe bemerkt hat, siehe z.B seine Tafeln zur Farbenlehre, Tafel V, die, abgesehen von den verblichenen Farben, viel Ähnlichkeit mit der Skizze hier hat).

Lichtfiguren

Wird Sonnenlicht an mehr oder weniger regelmäßigen Strukturen reflektiert, so kommt es zur Erscheinung von Lichtbahnen, Lichtsäulen oder Lichtstraßen. Neben geraden treten je nach den geometrischen Bedingungen auch krumme Linien auf.

Blickt man durch ein Gewirr von glänzenden Fäden in Richtung zur Sonne, so meint man, Kreisbögen um die Sonne zu sehen. Ebenso sieht man Lichtringe, wenn man durch die nassen Zweige eines kahlen Baumes zu einer Straßenlampe schaut, oder wenn sich eine Lampe in einer zerkratzten ebenen Fläche spiegelt. Völlig unregelmäßig orientierte Fäden oder Kratzer ergeben also scheinbar immer Kreise.

Wenn aber die zerkratzte spiegelnde Fläche nicht eben ist, sind die Figuren, die man sieht, keine Kreise mehr. Das ist mir neulich aufgefallen, als ich ein Spinnennetz in der Sonne glänzen sah.

Sich zu überlegen, welche Figuren auftreten können, strapaziert das räumliche Vorstellungsvermogen. Es ist hilfreich, erst einmal ein paar einfache Fälle anzusehen. Statt des Spinnennetzes betrachten wir eine unsichtbare gekrümmte Fläche, an die regellos glänzende Nadeln angeheftet sind, genauer gesagt: kurze Tangentenstückchen, deren Orientierung um den Berührungspunkt durch einen Zufallsgenerator bestimmt wird.

gegeben; die Sonne steht in der y-z-Ebene β=60° über dem Horizont, und das Auge des Beobachters befindet sich im Abstand H vom Koordinatenursprung im Punkt mit den Koordinaten (0, −Hcos(β), Hsin(β)) genau dort, von wo aus das Spiegelbild der Sonne im Ursprung zu sehen ist. Betrachtet wird ein quadratischer Bildausschnitt von 10 cm Seitenlänge.

Im linken Bild ist a=b=0, die Fläche ist also eben.
Im zweiten, dritten und vierten Bild ist a = 6E−3 cm⁻¹, b = 0, die Fläche hat also die Form einer seichten Rinne. Der Abstand H beträgt der Reihe nach 30 cm, 46.76 cm und 80 cm. Im dritten Bild befindet sich das Auge genau in der Brennlinie der parabolischen Rinne.
Bild 5 wurde mit a = 12E−3 cm⁻¹, b = −3E−3 cm⁻¹ und H = 120 cm erhalten, ein vom Mittelpunkt aus nach links und rechts ansteigender, nach oben und unten wenig abfallender, flacher Sattel.
Im sechsten Bild schließlich ist a = 6E−3 cm⁻¹, b = 4.5E−3 cm⁻¹ und H = 46.76 cm, die flache Mulde fokussiert das Sonnenlicht genau ins „Auge“ so dass alle angehefteten Nadeln glänzen. Diese Form kann allerdings bei Netzen, die aus gespannten Fäden bestehen, deren Gewicht vernachlässigbar ist, nicht auftreten.

Für die Reproduzierbarkeit der Ergebnisse seien hier die verwendeten Parameter angegeben: Die Länge der Nadeln beträgt 8 mm; zu sehen sind nur die Glanzstellen, für die gilt, dass sich der Winkel zwischen der Nadel und dem einfallenden Strahl von dem zwischen Nadel und Richtung zum Auge höchstens um 0.25° unterscheidet. (Der scheinbare Sonnendurchmesser beträgt 0.5°)

Echtes Gelb

Diese Zufallsbeobachtung ist von ganz anderer Art als alle bisher von mir beschriebenen. Ich habe etwas bei Youtube gefunden, was mich gewundert, aber nicht gefreut hat. Meine Suchmaschine, die mich anscheinend recht gut kennt, hat mir ein interessantes Video empfohlen. Es geht um den Sachverhalt, dass es gelegentlich strittig ist, ob eine bestimmte Farbe Blau oder Grün ist, und einige Hypothesen dazu. Aber zur Einführung ist erst einmal von Gelb die Rede. Da heißt es

„Nur: was Ihr hier [auf dem Bildschirm] seht, ist eigentlich gar kein richtiges Gelb. […] Also was ich hier sehe, ist echtes Gelb, das heißt: echtes gelbes Licht. […] jede Farbe hat eine bestimmte Wellenlänge, Rot ist längerwellig, violett ist kürzerwellig, und Gelb ist zwischendrin mit einer Wellenlänge von etwa 570 Nanometern je nach Gelbton. […] Wie kriegt man jetzt aus so einem breiten weißen Licht eine bestimmte Farbe, das heißt, eine bestimmte Wellenlänge? […] Das Licht […] trifft jetzt auf diesen Hintergrund. Der absorbiert das Licht, das heißt, er verschluckt es, bis auf eine Wellenlänge, […] die wird reflektiert …“

In Wahrheit ist Gelb die Farbe, mit der sich am besten zeigen lässt, dass die weit verbreitete Meinung „jede Farbe hat eine bestimmte Wellenlänge“ falsch ist. Dazu braucht man nur ein Prisma.

Es ist zwar so, dass es zu den meisten Farben auch Licht mit nur einer Wellenlänge und dem gleichen Farbton gibt (farbtongleiche Wellenlänge nach Helmholtz; die Ausnahme sind die Purpurfarben zwischen Rot und Violett). Aber damit eine von weißem Licht beleuchtete Oberfläche farbig oder auch nur hell erscheint, muss ein nennenswerter Bruchteil des einfallenden Lichts zurückgeworfen werden, bestimmt nicht nur „eine Wellenlänge“.

Für die folgenden Bilder musste eine der schönen gelben Blüten ein Blütenblatt opfern. Daraus wurde ein schmaler Streifen herausgetrennt und auf einer schwarzen Unterlage fotografiert. Erst einfach so, dann durch ein Prisma (erstes Bildpaar unten). (Die Versuchsanordnung habe ich in dem Abschnitt „Einfache Versuche mit einem Prisma“ schon früher beschrieben.)

Durch das Prisma sieht man das Spektrum des von dem gelben Streifen remittierten Lichtes. Von dem weißen einfallenden Tageslicht wird der rote und der grüne Anteil zurückgeworfen, der blaue Anteil wird verschluckt. Gelb als Oberflächenfarbe ist nämlich immer „Weiß minus Blau“, also die Summe von Rot und Grün. Gelb oder irgend eine andere Farbe mit nur einer Wellenlänge (gemeint ist ein winziger Wellenlängenbereich) kann es nur von selbstleuchtenden Lichtquellen geben.

Für das zweite Bildpaar wurde das erste Foto vom Bildschirm (LCD-Flachbildschirm) abfotografiert, im letzten Bild wieder durch das Prisma. Während das dritte von dem ersten Foto kaum zu unterscheiden ist, sieht das vierte doch recht anders aus als das zweite. Das liegt daran, dass das weiße Licht, das den Schirm hinterleuchtet, im Gegensatz zum Tageslicht aus nur wenigen schmalen Bändern und Linien besteht, mit einem Kontinuum nur im kurzwelligen, blau-violetten Bereich.

Aber da ist noch etwas: wenn ich durch das Prisma auf das linke Bild schaue, sehe ich die im letzten Bild noch schwach sichtbare blaue Linie nicht, dafür die grüne Linie deultich heller. Der Grund ist wohl der, dass die Empfindlichkeitskurven meines Fotoapparates nicht mit denen meiner Augen übereinstimmen. Darüber hinaus ist es nicht möglich, ein Spektrum exakt wiederzugeben, siehe dazu die Seiten über weißes Licht und die Prismenversuche.

Die spektrale Zusammensetzung des gelben Lichts vom Bildschirm unterscheidet sich von der des Lichts, das von der gelben Blüte reflektiert wird – aber das ist praktisch immer und bei allen Farben so, wenn sie auf irgend eine Weise reproduziert werden.

Schillerndes verwittertes Glas

Glas, das im Wasser oder in der Erde liegt, verwittert langsam. Alkali-Ionen werden aus der Oberfläche herausgelöst, die verbleibende Kieselsäure kristallisiert zum Teil, es bilden sich feine Risse, durch die Feuchtigkeit eindringt, und dünne Schichten blättern ab oder haften nur lose.

Jetzt habe ich eine Glasscherbe bekommen, die bei Gartenarbeiten gefunden wurde und in bunten Farben schillert. Es dürfte ein Stück vom Rand einer weiten, dickwandigen Schüssel sein. Wie lange es schon im Boden lag?

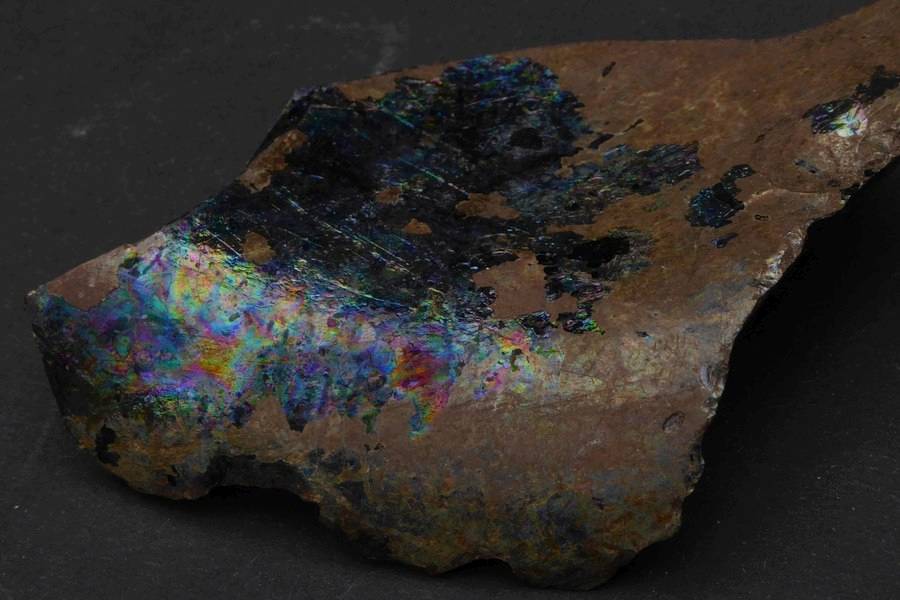
Das Bruchstück ist ca. 70 × 50 mm groß (diagonal gemessen) und an der dicksten Stelle ca. 9 mm stark. Die oberste, bräunliche Verwitterungsschicht blättert bei Berührung leicht ab, die Lagen darunter schillern unregelmäßig fleckig. Im Durchlicht sieht man davon wenig.

Glühender Himmel – Regenschein (zero order glow)

Ein leichtes Gewitter war vorbei, im Westen regnete es noch, da erstrahlte der Himmel in leuchtendem Rot. Die Sonne war von meinem Standpunkt aus nicht zu sehen, sie stand gerade noch 0.16° hoch (berechnet nach den Angaben in der Wikipedia), war also schon zum Teil unter dem Horizont.

Die Bezeichnung “zero order glow” leitet sich von der Klassifikation der Regenbögen ab, die Ordnung ist die Zahl der Reflexionen des Lichtes im Regentropfen. Das Licht, das wir hier sehen, wurde also nicht reflektiert, sondern nur durch Brechung aufgefächert, aber nicht wie beim Regenbogen in die Farben zerlegt. Ich habe so etwas schon einmal fotografiert („Hinterm Regenbogen“), damals stand die Sonne etwas höher (knapp 2°) und das Glühen daher nicht rot sondern orangegelb.

Rechts sind in der linken Bildhälfte die von der Sonne kommenden und die reflektierten Strahlen zu sehen, die den Regenbogen bilden, in der rechten Hälfte die wie durch eine dicke Sammellinse gebrochenen Strahlen.

Jeder der fallenden Regentropfen im Blickfeld liefert ein winziges Lichtpünktchen in der Farbe der untergehenden Sonne.

Farbige Lichtreflexe am Netz einer Baldachinspinne

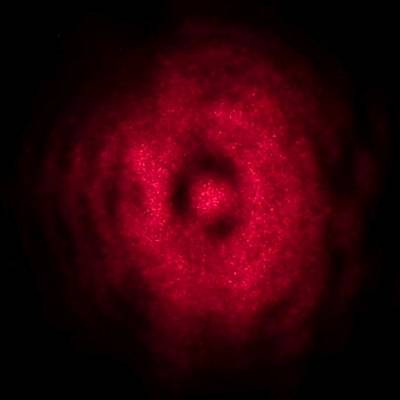
Neulich ist mir ein in geringer Höhe über dem Grund ausgebreitetes Netz einer Baldachinspinne aufgefallen, weil an ihm sehr deutlich glänzende Lichtbahnen und Lichtringe mit farbigen Reflexen zu sehen waren. Die folgenden Bilder zeigen zweimal denselben Bereich unter twas verschiedenen Winkeln fotografiert; rechts jeweils einen Ausschnitt aus dem linken Bild.

Das Netz – ein Gewirr aus Fäden innerhalb einer dünnen, leicht gewellten Schicht – erstreckt sich über den ganzen Bildbereich, aber man sieht die Fäden nur an den Glanzstellen. Es ergeben sich Lichtringe, die aber nicht wie meist kreisförmig sind, sondern oval – der Verlauf der gedachten Linien erinnert an Höhenlinien auf einer Landkarte. Ursache davon ist die Welligkeit der Schicht, in der die Fäden verlaufen; das soll aber hier nicht das Thema sein.

Neben weißen, also „farblosen“ Reflexen sind grüne und lila oder purpurfarbene zu sehen, andere Farben findet man nicht. Wie kommt es dazu?

Farben an Spinnennetzen sieht man meist im Gegenlicht vor einem dunklen Hintergrund; da zeigt das unter kleinem Winkel an den Fäden gestreute Licht die bunten Farben. Hier aber sind die Streuwinkel groß. Wäre von dem Fädengewirr eine Membran aufgespannt, würde sich die Sonne darin an den hellsten Stellen spiegeln, ähnlich wie im nebenstehenden Foto einer von einer Schnecke erzeugten Membran. Es liegt daher nahe, von Reflexion statt von Streuung zu sprechen.

Wie die Reflexion der Sonne an einem annähernd zylindrischen, transparenten Faden aussieht hängt von der Beobachtungsrichtung ab. Dazu werden rechts drei Makroaufnahmen von einem 1 mm starken Nylonfaden gezeigt. (a): nur eine Reflexion an der Vorderseite – der Winkel zwischen Beleuchtungs- und Beobachtungsrichtung (auf die zum Faden senkrechte Ebene projiziert) ist größer als der Regenbogenwinkel –, (b): links vom schmalen Reflex an der Vorderseite ist zusätzlich der doppelte Reflex von der Rückseite zu sehen, und ganz am rechten Rand auch noch Licht, das an der Rückseite zweimal reflektiert wurde. (Der doppelte Reflex von der Rückseite entsteht, weil es zwei verschiedene Strahlen gibt, die an der Rückseite reflektiert und um den gleichem Winkel abgelenkt werden, siehe die Skizze darunter. All dies erinnert an die Reflexion durch Regentropfen.) Im Bild (c) liegen die Fadenrichtung, Sonne und Beobachter in einer Ebene. Die Spiegelungen an Vorder- und Rückseite überdecken sich, und an beiden Rändern ist an der Rückseite zweimal reflektiertes Licht zu sehen.

Allerdings sind die Seidenfäden so dünn, dass die geometrisch-optische Behandlung mit Lichtstrahlen keine gute Näherung mehr ist. Die exakte Lösung für Lichtstreuung an einem transparenten Zylinder ist bekannt und in dem Standardwerk von van de Hulst [1] zu finden. Aber der Querschnitt eines Seidenfadens ist nicht exakt kreisrund. Beim Erstarren der Seide dürften sich Runzeln bilden, wodurch der besondere Glanz entsteht.

Wir wollen uns daher mit einer groben Abschätzung begnügen. Die Lichtwellen werden an der Oberseite des Fadens teilweise reflektiert, die in den Faden eingetretenen Wellen an der Unterseite. Die reflektierten Wellen überlagern sich. Der Wegunterschied zwischen den an Ober- und Unterseite reflektierten Wellenzügen ist etwas kleiner oder höchstens gleich der doppelten Fadendicke; der Wegunterschied mit dem Brechungsindex des durchlaufenen Materials multipliziert ergibt die Differenz der optischen Weglängen.

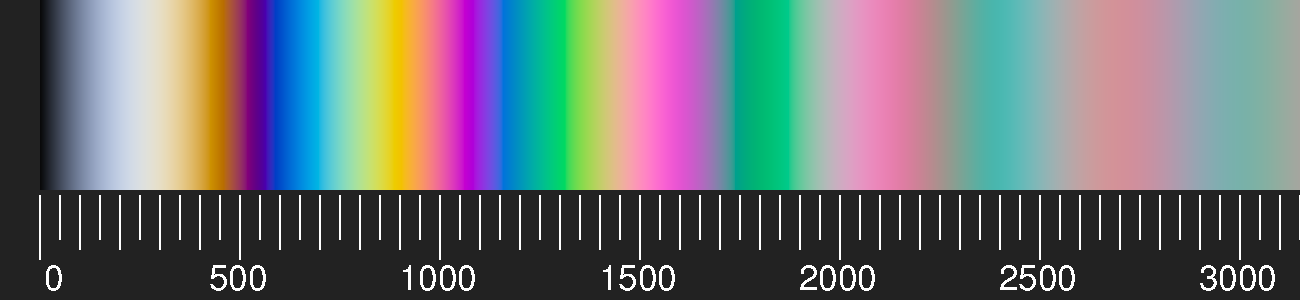
Interferenzfarben dünner Schichten, wie man sie z.B. an Seifenblasen beobachten kann, als Funktion der optischen Weglängendifferenz der Strahlen (in Nanometern, nm).

Vergleicht man die an den Seidenfäden auftretenden Farben mit der Skala für Zweistrahl-Interferenzfarben, so findet man, dass die optischen Wegdifferenzen ca. zwischen 1000 nm und 1300 nm liegen sollten oder aber (was ich wegen der intensiven Farben für weniger wahrscheinlich halte) zwischen 1500 und 1800 nm. Der Brechungsindex der Seide beträgt ca. n=1.5, daraus ergibt sich für die Dicke die untere Grenze von 330 nm für die lila schimmernden Fäden und 430 nm für die grünlichen (oder 500 beziehungsweise 600 nm). Das Besondere an diesem Netz war, dass die Dicke der Fäden sich über die glänzenden Stellen kaum änderte.

Die typische Dicke der Seidenfäden wird für Radnetzspinnen mit 1–4 μm angegeben [2], hier scheinen die Fäden aber noch deutlich dünner zu sein.

Im Zentrum der Lichtringe sind die Reflexe am hellsten und farblos oder nur ganz zart farbig. Dies dürfte zum Teil durch Überbelichtung zu erklären sein; bei den in Ost-West-Richtung verlaufenden Fäden ist die Reflexion farblos vom Typ (a), es fehlt also die interferierende Reflexion an der Unterseite des Fadens. (In den Bildern ist Süden oben; die Sonne stand 60.5° hoch im Süden, das Netz war annähernd horizontal, der Winkel zwischen Beleuchtungs- und Beobachtungsrichtung somit ca. 59°; der Regenbogenwinkel beträgt für n=1.5 ca. 26°.)

Literatur/Links

[1] H.C. van de Hulst (1957): Light Scattering by Small Particles. Dover Publications, New York, Inc. 1981, ISBN 0-486-64228-3

Schillerfalter

Der Große Schillerfalter (Apatura iris) ist in der Gegend, wo ich lebe, sehr selten. Vor kurzem konnte ich einen beobachten und fotografieren. Leider klappte er die Flügel nur ein paar mal für kurze Zeit auf (linkes Bild unten), und so konnte ich kein Bild erhalten, auf dem das Schillern zu sehen ist. Auf dem rechten Bild, das mir vor Jahren gelungen ist, sieht man immerhin ein Bisschen davon.

Schuppen auf den Flügeln

Schmetterlingsflügel sind mit zwei Lagen winziger, dachziegelartig übereinanderliegender Schuppen bedeckt, Grund- und darüberliegend die Deckschuppen. Die Schuppen sind hohl, mit glatter Unter- und feinstrukturierter Oberseite.

Rasterelektronenmikroskopische (REM) Aufnahmen der Schuppen auf dem Flügel eines Tagpfauenauges (Aglais io) mit steigender Vergrößerung. Das letzte Bild in der Reihe ist eine Detailvergrößerung aus dem vierten; die Bildbreite beträgt ca. 7 μm. (Zum Vergrößern klicken!) Fotos: SecretDisc, Quellen: Wikimedia commons a, b, c, d, Lizenz CC BY-SA 3.0

Rote, braune, orange, gelbe und schwarze Färbung der Flügel wird durch Pigmentierung der Schuppen hervorgerufen, Blau, Violett und Grün fast immer durch besondere Strukturen der Schuppen, die die Farben durch Interferenz erzeugen.

Über die Schillerfalter gibt es eine Arbeit von Pantelić et al.[1], aus der folgende elektronenmikroskopischen Aufnahmen stammen:

Raster- und Transmissions-Elektronenmikroskopische Aufnahmen von Schillerschuppen von A. iris. Links: Aufsicht von oben und Mitte: schräg von oben, rechts: Querschnitt. Wiedergabe aus [1] mit Genehmigung der OSA.

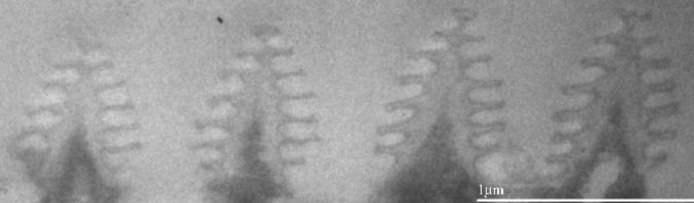
Es ist zu sehen, dass die Schillerschuppen von Apatura iris dem gleichen Bauplan folgen wie die Schuppen des Tagpfauenauges, nur sind die Proportionen sehr verschieden. Der Querschnitt der Leisten auf den Deckschuppen erinnert an die Form von Tannenbäumen. Je nach Beleuchtungs- und Beobachtungsrichtung sieht man Licht, das an mehreren übereinanderliegenden Schichten reflektiert wurde, das Schillern, oder eben nur das einfach remittierte Licht, braun infolge der Pigmentierung der Schuppen. Die Leisten stehen so dicht, dass die an den Nachbarn, nächsten Nachbarn etc. gestreuten Strahlen interferieren und so der Winkelbereich der Reflexion verkleinert wird. Pantelić et al.[1] stellen fest, dass das Schillern bei fester Beleuchtungsrichtung nur innerhalb eines kleinen Winkels zu sehen ist (sie geben 18° an) und dass das Maximum der spektralen Verteilung des reflektierten Lichtes bei 380 nm liegt, mit einer Halbwertsbreite von 50 nm. Der größte Teil der reflektierten Strahlung liegt also im ultravioletten Bereich, Schmetterlinge können das sehen, wir nicht.

Die Schillerschuppen der meistuntersuchten Falter, Morpho spp., sehen im Übrigen ganz ähnlich aus. Wie kommt es aber zu den völlig verschiedenen Erscheinungsbildern? Ein Grund ist natürlich, dass beim Schillerfalter die Reflexion hauptsächlich im UV erfolgt und wir nur einen Ausläufer der spektralen Verteilung sehen. Dies ist bei Morpho offensichtlich nicht der Fall. (Bei Morpho sind es nicht die Deck-, sondern die Grundschuppen, die schillern. M. rhetenor hat gar keine Deckschuppen auf den Flügeln.)

Zweitens sind die seitlichen Bänder an den Leisten gegeneinander versetzt (siehe das Bild rechts), darüber hinaus unterscheiden sich benachbarte Leisten mehr oder weniger zufällig ein wenig in der Höhe, so dass sich Interferenzeffekte herausmitteln [2], wodurch das Licht in einen größeren Raumwinkel hinein reflektiert wird und das Blau fast immer zu sehen ist. Die Deckschuppen sind transparent und gröber strukturiert, oder sie fehlen.

Links: Apatura iris mit gut sichtbarem Schillern. Foto Rosenzweig, Quelle: Wikimedia commons., Lizenz CC BY-SA 3.0.
Rechts: Morpho rhetenor cacica aus Südamerika. Exponat aus dem Insektenmuseum in Wunstorf/Steinhude. Die Spannweite dieses Falters beträgt ca. 15 cm.

Ähnlich aufgebaute Schuppen sind bei vielen Schmetterlingen vorhanden – nur merken wir meist nichts davon, weil die Reflexion im Ultravioletten erfolgt. So hat z.B. der orangefarbene Postillon (Colias croceus) Schuppen vom gleichen Typ wie der Schillerfalter mit tannenbaumähnlichem Querschnitt der Leisten.

Literatur

[1] Dejan Pantelić, Srećko Ćurčić, Svetlana Savić-Šević, Aleksandra Korać, Aleksander Kovačević, Božidar Ćurčić, and Bojana Bokić, “High angular and spectral selectivity of purple emperor (Lepidoptera: Apatura iris and A. ilia) butterfly wings”. Opt. Express 19, 5817–5826 (2011). doi:10.1364/OE.19.005817

[2] Shuichi Kinoshita, “Structural Colors in the Realm of Nature”, World Scientific Publishing Co. Pte. Ltd., ISBN-13 978-981-270-783-3

Sehr seltsame Interferenzfarben auf Eis

    Ein zugefrorener Moorsee irgendwo im Norden von Norwegen,
    auf dem neben der hellen Lichtstraße farbige Interferenzstreifen
    zu sehen sind.

Mika-Pekka Markkanen ist ein leidenschaftlicher Photograph, siehe seine Instagram oder fb-Galerien, und er hatte Kamera und auch Stativ bei sich.

Die Farben lassen sich durch Interferenz des an den Oberflächenstrukturen reflektierten Lichtes erklären. Diese seltsamen Strukturen entstanden vermutlich durch Schnee, der ins Wasser gefallen war kurz bevor es gefror. Die schwimmenden Schneekristalle ragen nur wenig über die Wasseroberfläche heraus, und so kann eine feine Skulptur der Eisoberfläche entstehen, die aus flachen Grübchen, Buckeln und Graten besteht. Wie das Licht daran reflektiert werden kann, wird im folgenden untersucht.

Klicken Sie auf die folgenden Vorschaubildchen, um vergrößerte Details und ein Einzelbild aus dem Video zu sehen!

Erklärungsversuch

Modellieren der Oberflächenstruktur

Die hervorstechendste Erscheinung auf den Bildern ist die helle Lichtstraße, die vom fernen Ufer auf den Beobachter zuläuft. Wäre das Eis vollkommen glatt, würde man nur das Spiegelbild der Sonne sehen. Lichtstraßen kann man häufig auf Wasserflächen sehen wenn die Sonne tief steht; ihre Form hängt von der Stärke der Wellen ab.

Das erste Bild in der Reihe unten zeigt, an welchen Stellen die Sonne sich spiegelt, wenn die Flächenelemente nicht geneigt sind (nur ein Punkt), um 3.5° geneigt sind (entlang der kleineren Kontur) oder um 8° geneigt sind. (Die Sonnenhöhe beträgt hier 10°, dies ist auf den Fotos auch näherungsweise der Fall.) Vergleicht man dies mit den Fotos, so sieht man, dass die meisten Facetten, die zur Lichtstraße beitragen, um weniger als 3.5° geneigt sind, aber ein kleinerer Teil weist Neigungen bis ca. 8° auf. Zufällig orientierte, um bis zu 8° geneigte Oberflächenelemente können aber nur Reflexe innerhalb der 8°-Kontur hervorrufen, auch wenn man eine zweite Reflexion berücksichtigt, und aus dem Bereich, wo die Farben gesehen werden, kommt in diesem Fall kein Licht zum Auge. Es müssen also Oberflächenelemente vorhanden sein, die so steil sind, dass sie nicht zur Lichtstraße beitragen, die aber das schon einmal reflektierte Licht in einen größeren Raumwinkelbereich reflektieren. Das zweite Bild unten zeigt den Bereich, in dem zweifach reflektiertes Licht gesehen wird, wenn zufällig orientierte Facetten mit 3.5° und mit 60° Neigung vorhanden sind (grauer Bereich). Man beachte, dass der höchste Punkt dieses Bereiches tiefer liegt als der Horizont. Das stimmt schon einmal mit den Fotos überein. Aber Farbe entsteht auf diese Art noch nicht.

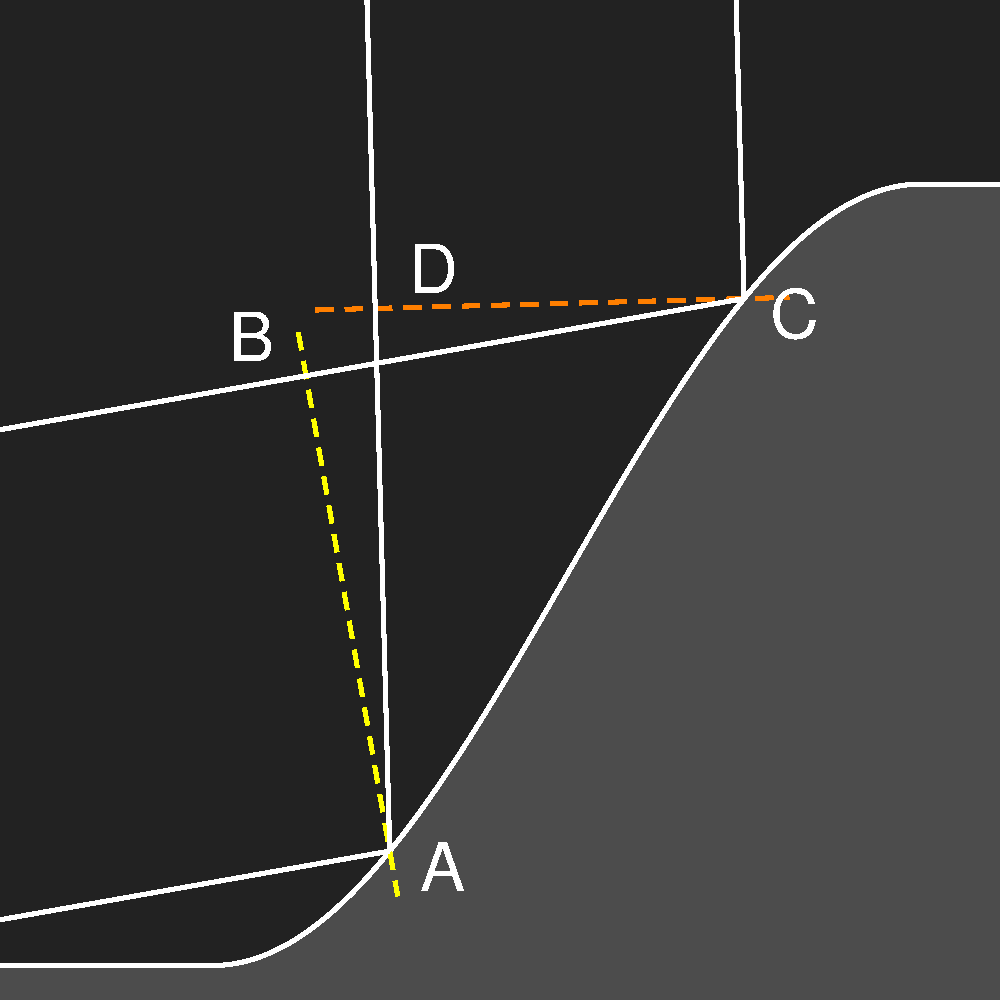
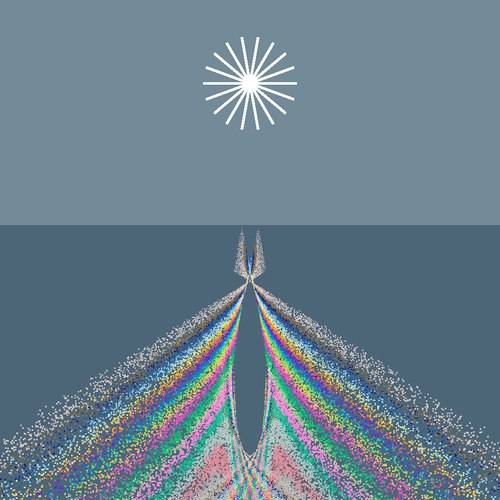
Farben treten auf, wenn es zu einer Glanzstelle mehr als einen Lichtpfad gibt, und wenn sich diese Pfade in der Länge ein wenig unterscheiden. Dann können durch Überlagerung der ankommenden Wellen Teile des Spektrums unterdrückt und andere verstärkt werden, das sieht man dann als Farbe. Wenn beispielsweise die Übergänge zwischen den flachen und den steilen Facetten keine scharfen Kanten, sondern Rundungen sind, kann dies schon geschehen. In der dritten Skizze oben sind zwei solche Lichtwege zu sehen. Das an einer horizontalen Fläche schon einmal reflektierte Licht komme von links; bis zu der gelben gestrichelten Linie sind beide Lichtwege gleich. Hinter der orangen gestrichelten Linie sind die Wege bis zum Auge wieder gleich lang. Aber die Strecken AD und BC sind etwas verschieden und so kommt es zu Interferenz.

Die vierte Skizze in der Reihe zeigt die Ergebnisse einer Modellrechnung, die die Erscheinungen auf den Fotos annähernd reproduziert. (Zum Vergrößern draufklicken!) Es wurde angenommen, dass das Licht zuerst an einer nur wenig geneigten Fläche reflektiert wird und dann auf die steile Flanke einer Stufe trifft, so wie im dritten Bild oben skizziert.

Während die Farben auf den Fotos im Vordergrund verblassen und verschwinden, ist dies bei der Simulation nicht der Fall. Der Grund ist einfach der, dass außer der Neigung der Facetten alle geometrischen Details ignoriert wurden, ebenso auch die Abhängigkeit der Reflexionskoeffizienten vom Einfallswinkel der Strahlung.

Folgende Parameter wurden für die Rechnung verwendet: die flachen Facetten sind um einen Winkel θ = 6° geneigt, ihre Orientierung φ ist zufällig. Der maximale Neigungswinkel der steilen Facetten relativ zu den flachen beträgt Θ_max = 60° (Θ reicht daher infolge der Abrundungen von 0° bis 60°), die Abrundungen werden durch eine Sinuskurve beschrieben wie in der obigen Skizze. Die Orientierung der steilen Flanken ist wie folgt festgelegt: Führt man ein mit den flachen Facetten verbundenes Koordinatensystem so ein, dass die z'-Achse senkrecht auf die Fläche steht und nach oben zeigt, die x'-Achse in die am steilsten abfallende Richtung zeigt, so hat die Flächennormale der Flanke in diesem System die Polarkoordinaten Θ und Φ, wobei Φ auf die Werte Φ = ±150° beschränkt ist. Die Gesamthöhe der Stufe ist H = 10 μm.

Die verwendeten Parameter lassen sich nicht aus der hexagonalen Symmetrie der Schneekristalle herleiten, dies ist ein großer Nachteil und zeigt, dass noch nicht die richtige Erklärung gefunden wurde. Aber diese Simulation kann ohnehin nicht die endgültige Lösung des Problems sein, weil die Höhe H der Stufen so gering ist, ungefähr 0.01 mm. Durch H wird die Breite der Interferenzstreifen bestimmt; je kleiner H ist, desto breiter sind die Streifen. Aber wenn Licht von so schmalen Facetten reflektiert wird, können Beugungseffekte nicht mehr vernachlässigt werden und die einfache Strahlenoptik (die hier verwendet wurde) liefert bestenfalls grobe Näherungen. Eine genauere Rechnung ist jedoch nicht einfach …

Der Poissonsche Fleck

„Um sich den theoretischen Ursachen für die vielfältigen unerklärbaren optischen Beobachtungen zu nähern, wurde 1818 von der französischen Académie des sciences ein Wettbewerb ausgeschrieben. Der 30-jährige Ingenieur Augustin-Jean Fresnel beteiligte sich bei diesem Wettbewerb mit einer neuartigen Arbeit über die Wellentheorie des Lichtes. Die Jury, der auch Siméon Denis Poisson angehörte, wurde von François Arago geleitet. Weitere Juroren waren der Mathematiker Pierre Simon de Laplace und die beiden Physiker Jean-Baptiste Biot und Joseph Louis Gay-Lussac.“ (laut Wikipedia)

Poisson, damals noch Anhänger der von Newton vertretenen Korpuskulartheorie des Lichtes, begutachtete Fresnels Arbeit und erkannte, dass danach im Mittelpunkt des Schattens eines Objekts mit kreisförmigem Umriss ein heller Fleck auftreten müsste, und hielt damit Fresnels Theorie für widerlegt. Arago jedoch führte den Versuch durch und fand den hellen Fleck, was schließlich dazu führte, dass Fresnel den Wettbewerb gewann. Arago wies später darauf hin, dass der Effekt schon im Jahr 1715 von Delisle [1] und 1723 von Maraldi [2] beschrieben worden war.

In Anbetracht der damaligen Möglichkeiten – man war auf die Sonne als Lichtquelle angewiesen – ist dieser Nachweis bewundernswert. Mit den heutigen künstlichen Lichtquellen und Digitalkameras ist es einfacher, wie man aus zahlreichen im Internet zu findenden Bildern schließen kann. Das ermutigte mich, es auch zu versuchen, und zwar mit möglichst einfachen Mitteln, um den Effekt endlich einmal mit eigenen Augen zu sehen.

Material

Als Lichtquellen eine LED-Taschenlampe mit Reflektordurchmesser 1 cm und ein kleiner Laserpointer, dazu eine Sammellinse mit 10 cm Brennweite; als schattengebende Objekte eine Magnetkugel mit 5 mm Durchmesser auf einer Stecknadel und Stecknadeln mit runden Köpfen von ca. 3.5 mm Dicke. Dazu ein Korkstöpsel, Holzklötzchen und ein Filmdöschen als Unterlagen, und als Bildschirm ein Blatt Papier an der Wand. Zwei Tische. Fotografiert wurde mit einer kleinen Digitalkamera auf einem Stativ.

LED-Taschenlampe, Taschenlampe mit Lochblende aus Alu-Klebefolie, Laserpointer mit vorangestellter Linse, Magnetkugel auf Stecknadel im Kork, Stecknadeln mit runden Köpfen

Versuchsanordnung

Der Abstand von der Lichtquelle zum Objekt betrug 3.40 m, der vom Objekt zum Schatten 1.30 m. Mit der Taschenlampe allein war das Schattenbild zu unscharf, um dem Poisson-Fleck zu sehen, daher wurde mit einer Nähnadel ein Loch von ca. 1 mm Durchmesser in eine Alu-Klebefolie gestochen und diese Lochblende vorne an der Lampe befestigt.

Um den Laserpointer leuchtend ablegen zu können, wurde der Druckschalter mit Klebefilm fixiert. Die vorangestellte Linse erzeugt aus dem Laserstrahl einen Lichtkegel.

Die Ergebnisse

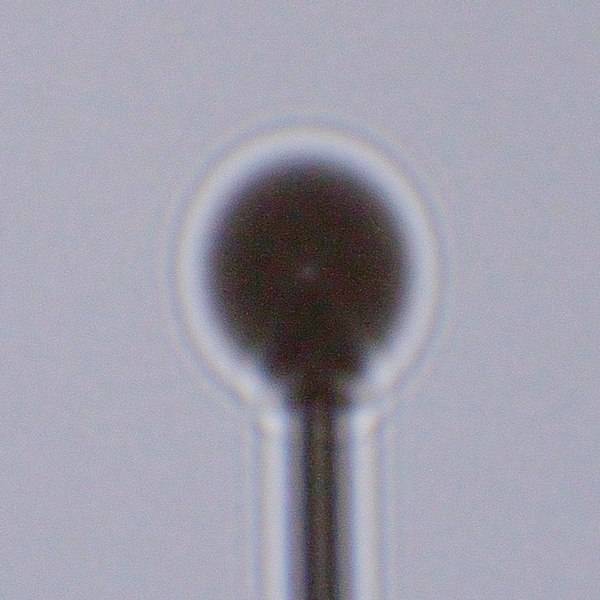
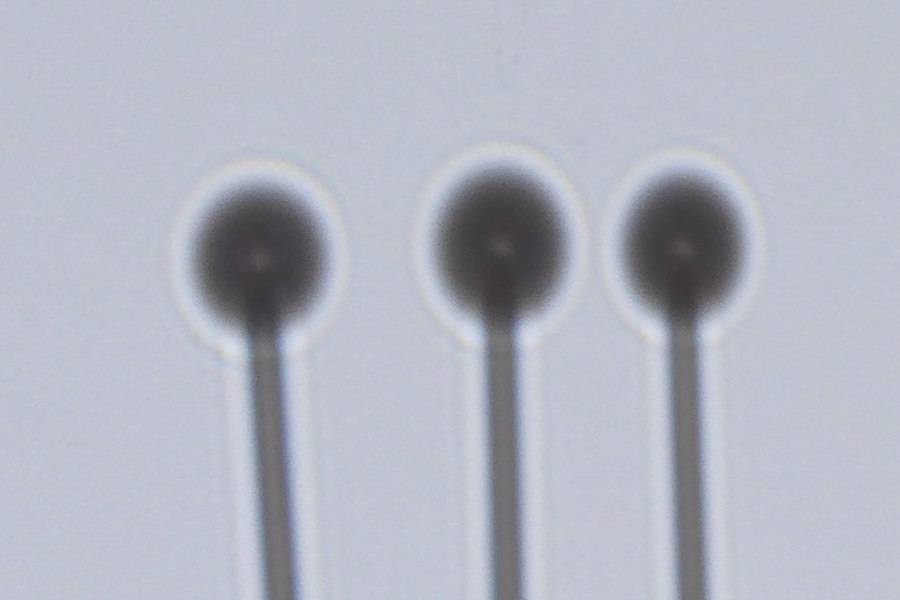
Mit freiem Auge sieht man die Flecken nicht sehr gut, aber auf den Fotos sind sie deutlich zu erkennen! (Vergrößern durch Klicken!)

Falsche Poisson-Flecken

Es gibt allerdings noch andere Möglichkeiten, helle Flecken in einem Schatten zu erzeugen. Beim Stöbern im Netz nach Bildern und Videos bin ich auf folgendes Beispiel gestoßen, das viel zu schön ist, um echt zu sein: eine CD, die transparente Mitte mit undurchsichtigem Klebeband überklebt.

Eine CD, die Mitte überklebt, und ihr Schatten – der Schatten, etwas länger belichtet – Rand der CD mit Millimeterpapier im Abstand von 15 mm als Hintergrund – dasselbe mit Scharfstellung auf das Millimeterpapier

Die Helligkeit in der Mitte des Schattens kommt nicht durch Fresnelsche Beugung zustande, sondern durch Brechung und Reflexion, ist also strahlenoptisch erklärbar. Die Scheibe hat nämlich einen durchsichtigen Rand. Das Bild rechts zeigt, was aus einem Lichtstrahl wird, der durch den Rand geht. Dazu wurde ein Laserstrahl in ungefähr derselben Richtung wie das Licht der Taschenlampe durch den äußeren Rand auf der linken Seite „bei 9 Uhr“ geschickt. Der größte Teil wird durch Brechung etwas nach außen abgelenkt – man beachte den hellen Ring auf dem linken Bild oben –, aber ein Teil wird an der leicht gekrümmten Außenfläche reflektiert und erhellt den Schattenbereich entlang einer Linie in radialer Richtung. In der Schattenmitte treffen sich diese Linien von allen Randpunkten, dort wird es am hellsten.

Fresnelsche Beugung

Der Nachweis des Poisson-Flecks, eines hellen Flecks im Schatten einer Kugel ist auch mit heutigen Mitteln nicht ganz leicht. Arago hat angeblich den Poissonschen Fleck hinter einem Scheibchen von 2 mm Durchmesser, das er auf eine Glasplatte geklebt hatte, gefunden.

Auch eine Kugel von 5 mm^ø ist nicht sehr bequem zu handhaben. Mit einer größeren Stahlkugel von 24 mm^ø konnte ich mit den mir zur Verfügung stehenden Mitteln den Lichtfleck nicht sichtbar machen. Wenn aber nur gezeigt werden soll, dass das Licht in den Schattenbereich hinein gebeugt wird, so geht das viel einfacher. Befindet sich das Auge im Schattenbereich der Kugel, so sieht man einen Teil des Randes infolge der Beugung hell. Wenn sich die Lichtquelle, der Kugelmittelpunkt und das Auge des Beobachters/der Kamera auf einer Linie befinden, dann fällt der Poissonsche Fleck auf die Pupille des Auges bzw. in die Blendenöffnung und dann erscheint der ganze Umfang hell.

Links eine LED-Taschenlampe und rechts ein Laserpointer, dessen Strahl durch eine Lupe aufgeweitet wurde, hinter einer Stahlkugel von 24 mm Durchmesser.

Solche Bilder kann man auch mit einer glattrandigen Münze, z.B. fünf Cent (Durchmesser 21.2 mm) erzeugen.

Fresnelsche Beugungseffekte sieht man gelegentlich auf Fotos, wenn glitzernde „Punkte“ unscharf abgebildet werden [1], [2]. Diese Beugungsmuster sind auf dem Sensor der Kamera winzig. Aber das gibt es auch größer: das verblüffende Gegenstück zum Poissonschen Fleck, nämlich ein dunkler Fleck in der Mitte eines Lichtflecks hinter eine Lochblende, lässt sich mit einem kleinen Laserpointer (und einer Lupe) sehr leicht zeigen und ist mit freiem Auge gut zu sehen.

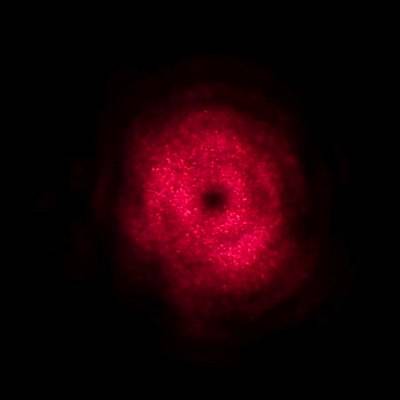
Linkes Paar: Beugungsmuster eines in eine Alu-Folie gestochenen, nicht ganz kreisrunden Loches von ca. 1 mm^ø. Die Mitte kann, je nach den Abständen zwischen Lichtquelle, Blende und Schirm, hell oder dunkel sein.

Rechtes Paar: Berechnete Beugungsbilder für eine kreisförmige Lochblende, Bildbreite je 2 cm. Lochdurchmesser 1 mm, Wellenlänge λ=650 nm, Abstand Lochblende–Schirm 1.5 m; Abstand der Punkt-Lichtquelle (vom Brennpunkt der Lupe aus zu messen) zur Blende 22.5 cm und 15 cm.

Überraschende Streifen – elliptische Polarisation

Über die Brillen zum Betrachten von 3D-Filmen habe ich schon einmal geschrieben [1] und einige seltsame Fotos gezeigt. Ich verwende so eine Brille gerne als handliches Polarisationsfilter, z.B. um die Polarisation des blauen Himmelslichtes zu sehen. Als ich bei Sonnenuntergang durch ein schräges Dachfenster schaue, halte ich die Brille zufällig nicht, wie meist, verkehrt herum, sondern so, wie man sie im Kino benutzt – und sehe das Fenster gestreift.

Links: die Sonne geht im Südwesten unter, das Licht vom blauen Himmel ist in südöstlicher Richtung größtenteins in vertikaler Richtung polarisiert. Verkehrt herum gehalten, lässt die Brille in dieser Stellung nur horizontal polarisiertes Licht durch, die Gläser erscheinen daher dunkel.

Mitte: durch die Brille, richtig herum gehalten, erscheint das Glas des schrägen Fensters gestreift. (Das linke Brillenglas lässt nur den linkszirkularen Anteil des Lichtes passieren, das rechte Glas den rechtszirkularen.)

Rechts: ein Brillenglas dicht vors Objektiv gehalten. Da das Fenster doppelt verglast ist, ergibt sich ein Moiré aus der Überlagerung der Streifen beider Scheiben. Außerdem sind auch breite Streifen senkrecht auf die schmalen zu sehen.

Es zeigte sich, dass die Streifen bei Veränderung des Beobachtungswinkels nicht wanderten, somit scheidet Interferenz auf Grund von Mehrfachreflexion an äußerer und innerer Scheibe als Ursache aus, denn diese Effekte sind stark winkelabhängig, siehe z.B. [2].

Die Fenster sind schon älter. Neuerdings wird bei solchen Fenstern für die Innenscheibe Verbund-Sicherheitsglas verwendet, für die äußere gehärtetes Glas. Hier aber sind allem Anschein nach Innen- und Außenscheibe aus gehärtetem Glas. Durch gezielte Wärme- und Kältebehandlung werden in solchen Glasscheiben innere Spannungen erzeugt, die im Fall eines Bruches das Glas in kleine Krümel zerspringen lassen, die nicht so gefährlich sind wie große Glassplitter. Anscheinend variieren die Spannungen periodisch.

Innere Spannungen machen Glas doppelbrechend; das einfallende linear polarisierte Licht wird in zwei senkrecht aufeinander schwingende Anteile aufgespalten, und beim Austritt aus dem Glas besteht eine Phasenverschiebung der beiden Anteile gegeneinander. Beträgt diese Verschiebung genau λ/4, so ist zirkular polarisiertes Licht entstanden, wie früher [1] beschrieben, im allgemeinen Fall ergibt sich elliptisch polarisiertes Licht, das als Überlagerung von zirkular und linear polarisiertem aufgefasst werden kann.

Goethes schwarzes und weißes Kreuz

Goethes Schriften zur Farbenlehre enthalten viele interessante und genau beschriebene Beobachtungen. Hier geht es um einen Nachtrag zur Farbenlehre aus dem Jahr 1820 (digitalisiert von Google), einen Aufsatz über die „Entoptischen Farben“, Farben, die, wie wir es heute verstehen, durch Doppelbrechung und Polarisation des Lichtes entstehen. Goethe wiederholt mit beträchtlichem Aufwand Versuche von Seebeck und von Brewster und beschreibt genau, wie er vorgegangen ist. Speziell zubereitete Glasplättchen werden verwendet, in denen das Licht vom blauen Himmel schwarze oder weiße Kreuze erscheinen läßt; mit einem schwarzen Spiegel (rückseitig geschwärzte Glasplatte) wird die Erscheinung noch gesteigert, mit zwei Spiegeln gelingt eine abermalige Steigerung.

Die Präparation der „entoptischen“ Gläser:
„man zerschneide eine mäßig starke Spiegelscheibe in mehrere anderthalbzöllige Quadrate, diese durchglühe man und verkühle sie geschwind. Was davon bei dieser Behandlung nicht zerspringt ist nun fähig entoptische Farben hervorzubringen.“

Der einfachste Versuch – das Glasplättchen liegt auf einem dunklen Untergrund, der blaue Himmel spiegelt sich darin und, je nach Blickrichtung, erscheint ein helles oder ein schwarzes Kreuz – ist am umständlichsten zu erklären, daher wenden wir uns zunächst den gesteigerten Versuchen zu.

Die schwarzen Spiegel dienen zur Polarisation des Lichtes beziehungsweise zur Feststellung der Polarisation. Goethe schreibt darüber nur, dass sie dazu dienen, das Licht zu dämpfen.

Die Behandlung der quadratischen Glasplättchen hat starke innere Spannungen zur Folge, die machen das Glas doppelbrechend und führen zu einem für das freie Auge unsichtbaren Muster, das zwischen Polarisationsfiltern sichtbar wird. Für die aufwendigeren Versuche mit den schwarzen Spiegeln verwendete Goethe einen „entoptischen Cubus“, einen gläsernen Würfel. Ob es mit einem gläsernen Spielwürfel auch geht?

Ein gläserner Würfel (a) auf schwarzer Unterlage, (b) im Durchlicht, (c) im Durchlicht zwischen gekreuzten Polarisatoren und (d) zwischen parallelen Polarisatoren. So ähnlich muss auch Goethe das schwarze und das weiße Kreuz in seinem Würfel gesehen haben.

Heute hat man bequemere Möglichkeiten, Versuche mit polarisiertem Licht anzustellen: der Flachbildschirm des Computers kann als Quelle linear polarisierten Lichts dienen, als Polarisationsfilter (Analysator) eignet sich auch die Brille, die man zum Anschauen von 3D-Filmen im Kino braucht (verkehrt herum gehalten), eine polarisierende Sonnenbrille oder, selbstverständlich, das Polfilter für den Fotoapparat.

Um etwas Ähnliches zu sehen braucht man auch keine „entoptischen Gläser“ mehr zu präparieren, sondern findet leicht irgendeinen Gegenstand aus Acrylglas oder einem anderen Kunstharz, der im Spritzgussverfahren hergestellt wurde. Besonders geeignet sind Becher, bei denen das Material im Mittelpunkt des Bodens eingespritzt wurde, oder runde Deckel.

Ein Plastikbecher vor dem weiß leuchtenden Bildschirm meines Computers, durch ein Polarisationsfilter fotografiert. Links ist die Durchlassrichtung des Filters senkrecht auf die Schwingungsrichtung des vom Bildschirm ausgehenden Lichtes und auf dem Boden des Bechers sieht man ein schwarzes Kreuz; im rechten Bild stimmt die Durchlassrichtung mit der Polarisation des Bildschirms überein, daher ist der Hintergrund hell, und es zeigt sich ein weißes Kreuz. (Die Polarisation des Bildschirms ist von der Vertikalen aus um 45° im Uhrzeigersinn gedreht.)

Um den Mittelpunkt herum sind die inneren Spannungen und die Orientierung der fadenförmigen Moleküle annähernd rotationssymmetrisch. Das hat zur Folge, dass Licht, das auf ein Flächenelement trifft, in einen Anteil, der in radialer Richtung, und einen anderen Anteil, der in tangentialer Richtung schwingt, aufgespalten wird. Nach dem Durchgang dieser beiden Anteile durch das Polarisationsfilter interferiert das, was von ihnen übrig bleibt und dadurch werden, je nach optischer Weglängendifferenz, Bereiche im Spektrum unterdrückt. Wenn aber das auftreffende Licht schon in radialer oder tangentialer Richtung schwingt, wird es nicht aufgespalten. Dies ist entlang zweier aufeinander senkrechter Durchmesser der Fall. So ergibt sich ein dunkles oder ein helles Kreuz, je nach Orientierung des Filters. (Etwas ausführlicher ist die Farbentstehung durch Interferenz in einem eigenen Aufsatz behandelt.) Das Spannungsmuster in Goethes geglühten und abgeschreckten quadratischen Glasstückchen ist zwar nicht rotationssymmetrisch, hat aber doch die Symmetrien des Quadrates, und das führt auf ganz ähnliche Kreuze.

Goethe beschreibt diese Beobachtungen genau, ist in den Deutungs- und Erklärungsversuchen aber ganz in seinen Vorstellungen über die Farbentstehung gefangen.

Jetzt zu dem einfachsten Versuch, bei dem das „entoptische Glas“ auf einer dunklen Unterlage horizontal liegt, das Himmelslicht spiegelt und unter einem schrägen Winkel betrachtet wird. Das Licht vom blauen Himmel ist teilweise polarisiert. Wir betrachten zunächst den Fall, dass das elektrische Feld in der Einfallsebene, die durch die Strahlrichtung und die Senkrechte aufgespannt wird, schwingt (p-Polarisation). Liegt der Einfallswinkel in der Nähe des Brewster-Winkels, so wird das Licht an der Oberfläche kaum reflektiert. Es dringt ins Glas ein und wird dabei in zwei aufeinander senkrecht schwingende Strahlen (ordentlicher und außerordentlicher Strahl) aufgespalten. Die Reflexion an der Unterseite wirkt wegen der Nähe zum Brewsterwinkel wie ein Polarisationsfilter, und es liegt somit wieder ein doppelbrechendes Medium zwischen zwei Polarisatoren vor, das erste „Filter“ ist der Streumechanismus, der das Himmelslicht polarisiert, das zweite liegt in der Reflexion an der Unterseite. Es entstehen also Farben und auch das schwarze Kreuz. Schwingt das Licht dagegen in horizontaler Richtung, also senkrecht auf die Einfallsebene (s-Polarisation), so erscheint das weiße Kreuz.

Statt des blauen Himmels wurde für die folgenden beiden Bilder wieder der Computerbildschirm verwendet; die Aufnahmen entstanden ohne Polarisetionsfilter, man sieht die Farben mit freiem Auge genau so.

Mit einigem guten Willen sieht man im linken Bild das schwarze Kreuz, im rechten das weiße. Da das Licht vom Bildschirm schräg polarisiert ist, musste ich meinen „entoptischen“ Plastikdeckel schräg stellen, um die beiden Erscheinungen zeigen zu können.

Das schwarze Kreuz ist also zu sehen, wenn das schräg einfallende Licht in Bezug auf die reflektierenden Flächen überwiegend p-polarisiert ist, das weiße, wenn die s-Polarisation vorherrscht.

Goethe war von den zwischen polarisierenden Spiegeln an Glas, Glimmerblättchen und Kristallen auftretenden Farben begeistert, wie man dem folgenden Gedicht entnehmen kann:

Entoptische Farben

An Julien

Laß dir von den Spiegeleien
Unsrer Physiker erzählen,
Die am Phänomen sich freuen,
Mehr sich mit Gedanken quälen.

Spiegel hüben, Spiegel drüben,
Doppelstellung, auserlesen;
Und dazwischen ruht im Trüben
Als Crystall das Erdewesen.

Dieses zeigt, wenn jene blicken,
Allerschönste Farbenspiele;
Dämmerlicht das beide schicken,
Offenbart sich dem Gefühle.

Schwarz wie Kreuze wirst du sehen,
Pfauenaugen kann man finden;
Tag und Abendlicht vergehen,
Bis zusammen beide schwinden.

Und der Name wird ein Zeichen,
Tief ist der Crystall durchdrungen:
Aug' in Auge sieht dergleichen
Wundersame Spiegelungen.

Laß den Macrocosmus gelten,
Seine spenstischen Gestalten!
Da die lieben kleinen Welten
Wirklich Herrlichstes enthalten.

Buntes Schwarz II: Vinylschallplatten

Die farbigen Reflexe auf CDs sind heutzutage eine alltägliche Erscheinung. Ähnliche Farben konnte man aber auch schon früher an den Vinyl-Schallplatten beobachten, allerdings nur unter streifendem Lichteinfall. Rechts ein Foto, das ungefähr 1960 entstanden ist.

Als ich eine alte Schallplatte (die ich ohnehin nicht mehr abspielen kann) für den Bau einer Influenzmaschine zweckentfremdet habe, sah ich zu meiner Überraschung schwache Farbstreifen im Licht eines Punktstrahlers, und zwar bei nahezu senkrechtem Lichteinfall.

Die Farben erinnern entfernt an Queteletsche Ringe oder Farben von dünnen Schichten. Daher vermute ich auch hier die Interferenz von Strahlen, die ein wenig verschiedene Wege zuzrücklegen und am selben Punkt auf der Netzhaut im Auge auftreffen. Das könnten Strahlen sein, die in den Rillen zweifach reflektiert werden, wie am Ende dieses Abschnittes skizziert, und Farben hervorrufen, wie man sie von Seifenblasen, Ölfilmen auf nasser Straße und anderen Fällen von Zweistrahlinterferenz kennt.

Mit einer LED-Taschenlampe habe ich diese Erscheinung an mehreren alten Vinylplatten untersucht. Dabei zeigte es sich, dass unter ganz ähnlichen Bedingungen die Ergebnisse recht unterschiedlich ausfallen, wohl in Abhängigkeit vom Rillenquerschnitt. Unten einige Beispiele.

Das letzte Bild in der Reihe zeigt die Platte, an der ich diesen Effekt zuerst gesehen habe (die den erfolglosen Test als Scheibe einer Influenzmaschine mit geringen Blessuren überstanden hat). Die Bilder lassen sich durch Klicken vergrößern!

Die Reihenfolge der Farben unterscheidet sich deutlich von der, die man an Seifenlamellen oder anderen Beispielen von Zweistrahlinterferenz sehen kann, ganz so einfach scheint die Erklärung also doch nicht zu sein. Die Rillen sind ja so schmal, dass Beugungseffekte nicht vernachlässigbar sind. Statt nur die strahlenoptischen zwei Lichtwege zu berücksichtigen, wo die Strahlen an den Seitenflächen der Rillen gespiegelt werden, sollte man die Elementarwellen im Sinne von Huygens und Fresnel betrachten, die von allen Punkten entlang des Rillenquerschnittes ausgehen, dann ein zweites Mal gestreut werden und schließlich die auslaufende Welle bilden.

Wir haben gesehen, dass winzige Oberflächenteile von schwarzem Papier in verschiedenen Farben glänzen; die Oberfläche ist im Kleinen unregelmäßig strukruriert, und entsprechend ist das Muster von bunten Pünktchen ebenfalls ganz unregelmäßig. Hier aber weist die Oberfläche leicht wellige Rillen auf, deren Querschnitt konstant ist. Wenn man bei gegebenem Beleuchtungs- und Beobachtungswinkel an einem Punkt eine bestimmte Farbe sieht, dann wird sich in Richtung der Rillen die Farbe nur sehr langsam ändern, und ebenso ist in den benachbarten Rillen fast dieselbe Farbe zu erwarten. Die doch recht regelmäßige Struktur der Oberfläche führt führt auf ein geordneteres Muster von Interferenzfarben.

Geometrische Veranschaulichung der Lichtstreuung durch eine Rille mit parabolischem Querschnitt. Ein einfallendes Bündel von parallelen Strahlen wird von dem schwarzen, aber glänzenden Material reflektiert. Die vollständige Skizze links ist etwas unübersichtlich, daher werden im zweiten Bild nur die einfallenden und die nur einmal reflektierten Strahlen gezeigt, im dritten in der Reihe dann nur die nach der zweiten Reflexion auslaufenden Strahlen. Es sind also drei auslaufende, divergierende Strahlenbüschel vorhanden, wobei die Wegdifferenz der nach nur einer Reflexion auslaufenden Strahlen (mittleres Bild) zu den beiden anderen vermutlich zu groß ist, um merkliche Interferenzfarben hervorzurufen.

Buntes Schwarz

Ein Bogen schwarzes Kartonpapier in Licht der Sonne. Es sieht nicht auffällig aus, schwarz eben, genauer gesagt: dunkelgrau. Aber wenn man genau von Nahem in der Richtung zur Sonne darauf schaut, so zeigt sich ein wirres, buntes Pünktchenmuster. Rechts ein Detail aus dem linken Bild. Am unteren Rand ist die Millimeter-Teilung eines Zeichendreiecks aus Acrylglas zu sehen.

Ich erinnere mich: diese Erscheinung hat doch schon Goethe beschrieben. Goethes Werk „Zur Farbenlehre“ kann man gescannt und digitalisiert im Internet im Deutschen Text-Archiv finden, hier ist die Stelle:

373. Läßt man ein polirtes Silber durch Scheidewasser
dergestalt anfressen, daß das darin befindliche Kupfer
aufgelöst und die Oberfläche gewissermaßen rauh wer-
de, und läßt alsdann das Sonnenbild sich auf der
Platte spiegeln, so wird es von jedem unendlich klei-
nen erhöhten Puncte einzeln zurückglänzen, und die
Oberfläche der Platte in bunten Farben erscheinen.
Eben so, wenn man ein schwarzes ungeglättetes Papier
in die Sonne hält und aufmerksam darauf blickt, sieht
man es in seinen kleinsten Theilen bunt in den lebhaf-
testen Farben glänzen.

Von Goethe ist keine zutreffende Erklärung zu erwarten; Beugung und Interferenz sind die Ursachen, siehe den Abschnitt über Beugung, wo das genauer erklärt wird.

Das nächste Bildpaar zeigt buntes Glänzen im dunkelbraunen Fell eines Hundes. Die Erklärung ist dieselbe; die Farben sind dort zu sehen, wo sich die Glanzstellen etwas außerhalb des Schärfebereiches befinden.

367. Wenn man eine feine Stahlsaite vom Röllchen
abnimmt, sie ihrer Elasticität gemäß verworren durch
einander laufen läßt und sie an ein Fenster in die
Tageshelle legt, so wird man die Höhen der Kreise und
Windungen erhellt, aber weder glänzend noch farbig
sehen. Tritt hingegen die Sonne hervor, so zieht sich
diese Hellung auf einen Punct zusammen, und das
Auge erblickt ein kleines glänzendes Sonnenbild, das,
wenn man es nahe betrachtet, keine Farbe zeigt. Geht
man aber zurück und faßt den Abglanz in einiger Ent-
fernung mit den Augen auf, so sieht man viele kleine,
auf die mannigfaltigste Weise gefärbte Sonnenbilder, und
ob man gleich Grün und Purpur am meisten zu sehen
glaubt, so zeigen sich doch auch, bey genauerer Auf-
merksamkeit, die übrigen Farben.

Zufallsbeobachtungen

Reflexe an einem Spinnennetz

Schmelzendes Eis

Sehr seltsame Interferenzfarben auf Eis, zweiter Versuch

Regenbogenwurm

Anatomische Details

Die Ursache des Irisierens

Beugung an einem Kreuzgitter

Dünnschicht-Interferenzfarben

Welcher Wurm?

Beugung und Interferenz an behauchter Fensterscheibe

Der Simulationsversuch

Fluoreszierende Bananen

Regenbogenfarben

Doppelbrechung und Polarisation, Komplementärfarben

Elliptische Polarisation, Zirkularpolarisation

Lokale Adaptation, Nachbilder

Beugungsmuster am Fliegenauge

Das Negativ

Panorama mit Mond

Abendrot, Himmelsfarben

Weißabgleich

JPEG-Kompression

Eisblumen

Schilfrohr

Lichtringe

Interferenzfarben

Fresnelsche Beugung

Leuchtende Nachtwolken

Wiedergabetreue

Die Farben

Gespiegeltes Eis

Strahlen und von unten beschienene Wolken

Gekrümmte Lichtstrahlen

Terrestrische Refraktion

Glastürprisma

Lichtfiguren

Echtes Gelb

Schillerndes verwittertes Glas

Glühender Himmel – Regenschein (zero order glow)

Farbige Lichtreflexe am Netz einer Baldachinspinne

Literatur/Links

Schillerfalter

Schuppen auf den Flügeln

Literatur

Sehr seltsame Interferenzfarben auf Eis

Erklärungsversuch

Modellieren der Oberflächenstruktur

Der Poissonsche Fleck

Material

Versuchsanordnung

Die Ergebnisse

Falsche Poisson-Flecken

Fresnelsche Beugung

Überraschende Streifen – elliptische Polarisation

Goethes schwarzes und weißes Kreuz

Entoptische Farben

Buntes Schwarz II: Vinylschallplatten

Buntes Schwarz

Zu den früheren Beobachtungen … klick!