| Dietrich Zawischa | Kontakt |
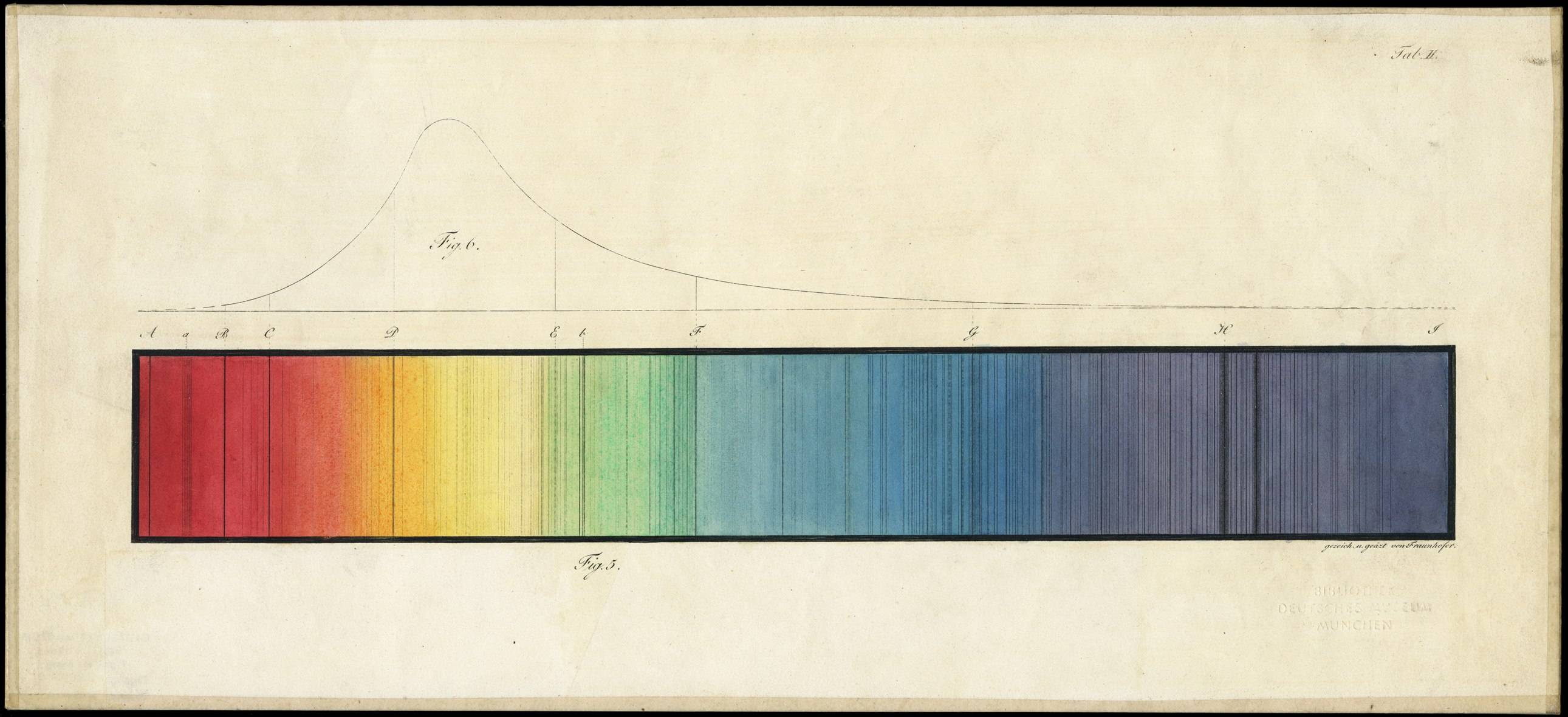
Zunächst zwei Bilder, die staunenswert sind. Die Fraunhoferlinien im Sonnenspektrum.

Handkolorierte Zeichnung von Joseph von Fraunhofer. Foto: Deutsches Museum. Zum Vergrößern draufklicken! (In noch höherer Auflösung finden Sie dieses Bild unter dem angegebenen Link zum Deutschen Museum.)
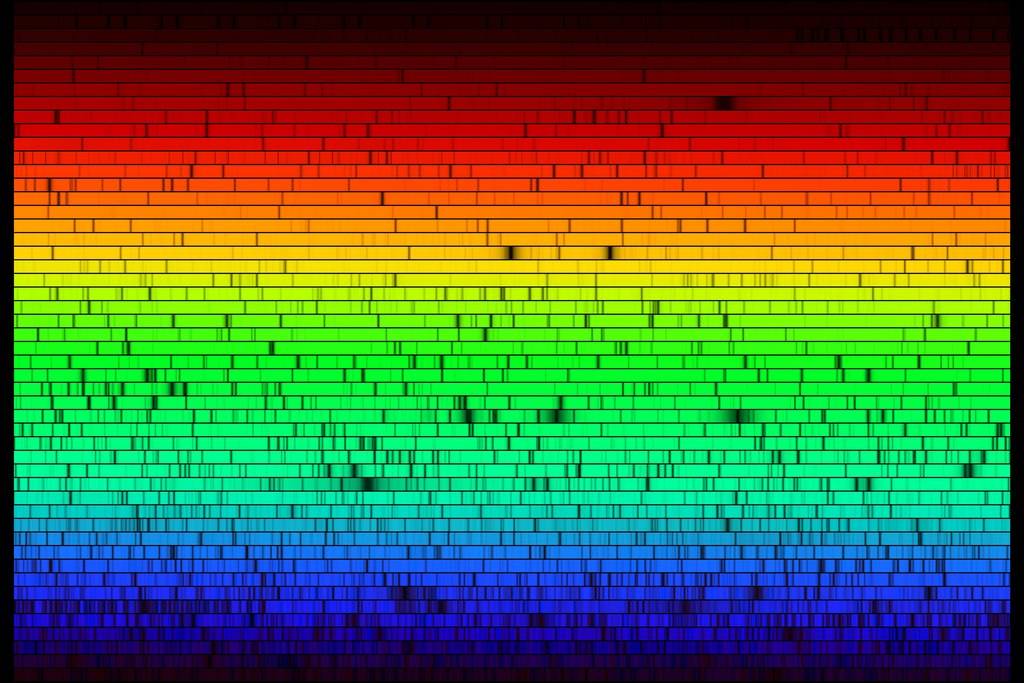
Hochaufgelöstes Spektrum des Sonnenlichts, erzeugt aus Daten, die mit einem Fourierstransform-Spektrometer erhalten wurden. In der Darstellung wird ein Échelle-Spektrum nachgeahmt. Jeder der 50 Streifen überdeckt einen Wellenlängenbereich von 6 nm; die Wellenlänge nimmt von unten nach oben zu, entlang der Streifen von links nach rechts. Gezeigt wird der sichtbare Bereich von 400 bis 700 nm. Quelle: NASA
Um zu überprüfen, ob die Fraunhoferlinien auch im Umkehr- oder Stegspektrum zu sehen wären, wurden in einer Modellrechnung Spalt- und Stegspektrum eines energiegleichen Spektrums mit einer Lücke für verschiedene Spaltbreiten einander gegenübergestellt. Für die Rechnung wurden die Spektralwertkurven des CIE-1931 Normalbeobachters verwendet, für die Darstellung der sRGB-Farbraum zugrundegelegt.
Da man Spektren prinzipiell nicht exakt im Bild reproduzieren kann, sehen die Farben der hier gezeigten Bilder nicht genau so aus wie die, die man im Experiment sieht. Das Stegspektrum lässt sich allerdings auf dem Bildschirm getreu wiedergeben (Link), wenn man die Helligkeit etwas reduziert.


Links: oben ein breiter weißer „Spalt“, in der zweiten Reihe das dazugehörige Newtonsche „Vollspektrum“ darunter das sogenannte Stegspektrum und ganz unten der zugehörige schwarze Streifen, „Steg“ vor weißem Hintergrund. Dass aus dem energiegleichen Spektrum ein Wellenlängenbereich von zwei Nanometern Breite herausgeschnitten wurde, ist bei dieser Spalt- bzw. Stegbreite nicht zu sehen.
Rechts: dasselbe mit schmälerem Spalt bzw. Steg. Um ein gut sichtbares Spektrum zu erhalten, wird die Helligkeit des Spalts erhöht (was auf dem Bildschirm nicht gezeigt werden kann). Das Stegspektrum ist hier schon recht blass; es ist mit der größtmöglichen Helligkeit wiedergegeben.


Bei weiterer Verringerung der Spaltbreite (und Erhöhung der Helligkeit) nähert sich das Newtonspektrum dem exakten Spektrum an und man erkennt deutlich den herausgeschnittenen Bereich. Im Stegspektrum ist der fehlende Bereich als helle Linie kaum mehr zu sehen. (Zum Vergrößern aufs Bild klicken!)
Würde man dieses synthetische Spektrum genau so hoch aufgelöst zeigen wie jenes in dem zweiten Bild oben, so wäre in einem der orangegelben Streifen genau ein Drittel schwarz! Alle Absorptionslinien sind viel schmäler als die hier zum Testen der Sichtbarkeit verwendete Lücke von 2 nm, die in dem bei der nötigen Auflösung verblassten Stegspektrum kaum mehr zu sehen ist.
Goethe hat in einem Aufsatz über den Regenbogen seine Meinung geäußert, eine schwarze Scheibe statt der Sonne in einem gleißend hellen Himmel würde einen umgekehrten Regenbogen entstehen lassen, etwa so, wie es in den folgenden Bildern das das zu dem linken Bild gehörige Negativ rechts zeigt.


Ein Bild von einem Regenbogen kann man also invertierten, indem man es in ein Negativ umrechnet. Aber wenn man mit riesigem Aufwand einen gleißend hellen Himmel mit einer dunklen Sonne darin simulieren würde und dann in einem Sprühnebel einen invertierten Regenbogen sehen wollte, würde man enttäuscht. Einfach deshalb, weil die dunkle Sonne die Beleuchtung nur unmerklich verringern würde.
Um abzuschätzen, welcher Bruchteil der Beleuchtungsstärke dem Regenvorhang (oder Sprühnebel) fehlt, wenn am gleißend hellen Himmel ein kreisförmiges Stück nicht leuchtet, findet man in einer nicht allzu komplizierten Rechnung, dass das Verhältnis des fehlenden Beitrages der schwarzen Scheibe zur Beleuchtungsstärke durch den Himmel durch das Quadrat des halben Winkels (im Bogenmaß) gegeben ist, unter dem man die Scheibe sieht. Der scheinbare Radius der Sonnenscheibe beträgt ca. 0.27°, also 0.27π/180. Das Ergebnis ist 2.2×10−5, also ungefähr 0.0022%. Auch ohne eine genauere Rechnung lässt sich sagen, dass der Unterschied zu der Situation ohne die schwarze Sonne am gleißenden Himmel nicht wahrnehmbar wäre.
Um die Idee von der Symmetrie oder Polarität zwischen Licht und Finsternis zu widerlegen, braucht es keine komplizierten Erscheinungen wie den Regenbogen oder Versuche mit Prismen. Würden Gegenstände helle Schatten werfen, wenn der Himmel gleißend hell und die Sonne dunkel wäre? Ja, wenn man den Helligkeitsanstieg von ca. 0.0022% am Rand des „Schattens“ bemerken könnte.
Ist es etwa so, dass von Symmetrie und Polarität auch noch gesprochen werden kann, wenn der eine Pol sehr auffällig, der Gegenpol hingegen nur mit modernster Messtechnik nachzuweisen ist?
Zum Artikel „Farbenstreit-Wiederbelebungsversuche“ oder zur Eingangsseite