Refraction and dispersion of light
The html formatting and custom instructions have been disabled on this server. The same file with adapted formatting can be found here: https://farbeinf.de/static_html/refraction.html.

Image: In a darkened room a pencil of light prepared by slit-shaped diaphragms is directed onto a glass prism. The prism is placed on white paper to make the path of the light and its spreading visible. The light finally falls on a tilted piece of white cardboard, showing the spectrum. The spreading is due to the fact that the index of refraction of the glass depends on the wavelength of the light. This dependence of the refractive index on wavelength (or frequency) is called dispersion, and is the source of several beautiful atmospheric colour phenomena.
The rainbow

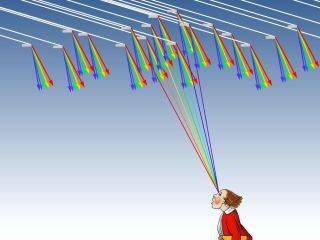
A very conspicuous phenomenon with a not-so-simple explanation, the rainbow, comes from reflection and refraction of the sunlight in the falling drops; its colours are mainly due to dispersion, which means that the refractive index of water depends on the wavelength of light.
Goethe, in a section on the rainbow of his treatise on colours (Farbenlehre) sketches the historic progress of insight:
Rainbow
. . .
In the oldest times the iris was believed to be a reflection of the sun in a dark cloud.
We skip what else the ancient have thought or said.
Seneca hit on the lucky idea that it might be an infinite repetition of the sun's image.
Antonius de Dominis [perished 1624] realises first, what exactly happens in each single drop.
. . .
Descartes develops in more detail than the latter the reflection which is connected with refraction, and by this explains the second bow; . . .
René
Descartes gave 1637 the explanation on the basis of ray optics (geometric optics),
George B. Airy succeeded in
1838 to give a detailed (but approximate) description including diffraction and interference effects. Gustav Mie finally in 1908 presented the exact solution for the scattering of light by dielectric spheres – a solution which nowadays can be evaluated with fast computers, but which does not give an intuitive explanation for the calculated phenomena.
(There is a special section devoted to Mie scattering.)
Beautiful images of rainbows and other atmospheric phenomena may be found in the web at the following sites:
www.meteoros.de, www.nachtwolke.de,
www.allthesky.com,
Atmospheric Optics,
Paraselene
– and many more; also the geometric-optical explanation is to be found at several places, while interference and diffraction phenomena in most cases are only mentioned. Here these shall be considered too.
What is happening?
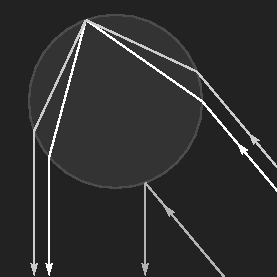 |
A water-filled spherical vase serves as a model for a falling raindrop (following Antonius de Dominis, Descartes and Goethe). Instead of the sun, a small lamp shines on the drop, its mirror image on the front surface is seen as a white point to the right of the centre. Light which enters the drop is reflected at the back surface and leaves the drop to finally reach the eye of the observer. This can happen along two different paths, and correspondingly two reflexes are seen on the left side of the drop.
The sketch to the left corresponds to the image just below it. |



The left image shows a drop well inside of the rainbow, where the sky is brighter than outside. Increasing the angle of observation (measured from the point opposite to the sun), the two reflections approach each other (middle image), join while becoming very bright – and eventually vanish. As the shortest waves are refracted most, first the "blue" rays join and get bright while green and red are still separated. Then green becomes bright and vanishes, and finally red (right image). What we see as a rainbow are the tiny, but (in the light of the sun) very bright reflections in the innumerable falling drops.
The fact that from each drop two beams reach the eye and are added there, causes the interference fringes seen at the inner side of the bow in the pictures below.
Light that is twice reflected before it leaves the drop produces the second bow.
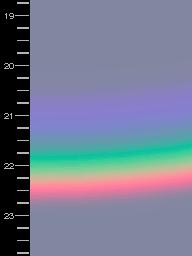
The following pictures show the colours of the rainbow, computed for different drop sizes. From the appearance of the bow, one can get a fair estimate of the average diameter of the drops. The scale gives the angle, measured from the point opposite to the sun.



 Droplet diameters, from top to bottom: 2 mm, 1 mm, 0.7 mm, 0.5 mm
Droplet diameters, from top to bottom: 2 mm, 1 mm, 0.7 mm, 0.5 mm
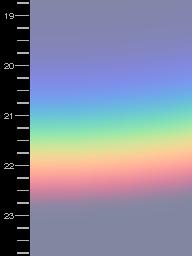
If the drop-sizes are not very uniform, the interference fringes (supernumerary bows) are washed out.

Computed colours for a mixture of different droplet sizes. A Gaussian distribution has been assumed, mean diameter 0.5 mm, standard deviation 0.06 mm.
For details of the computation of the above figures see the section on Mie scattering.

Rainbow with supernumeraries
Refraction by ice crystals
The colours of the rainbow are primarily due to refraction and dispersion of light by the raindrops, but the correct explanation is somewhat involved. Colours from refraction by ice crystals in the air are easier to understand, but as ice crystals may have different shapes and can float in the air in preferred orientations or randomly oriented, there are many different possible phenomena. Here we deal only with the simpler and more frequent ones; details on the rare events may be found on the site Atmospheric Optics of Les Cowley.
Circumzenithal arc

Circumzenithal arc seen in Wunstorf (Germany), October 9th 2006, 10:45 CEST,
at a solar height of 23.9º. The red side of the arc is closest to the sun. (
More pictures)
CZA and CHA are the most colourful arcs. Both are due to refraction by 90º ice prisms which split the white light into the spectral colours. If the ice crystals are flat hexagonal prisms, they tend to orient themselves such that bases are horizontal when they float in the air. Light rays entering the crystal through the top plane and leaving through one of the sides produce the CZA; light entering from the side and leaving through the bottom plane make the CHA. Centre of both bows is the zenith, but the CHA is close to the horizon.
However, even these arcs do not exhibit spectral colours for several reasons. First of all, they appear before a background of blue sky with thin clouds (this is a great advantage for the reproduction of the colours on the screen), on the other hand, the finite angle of the sun's disc, the not exactly horizontal orientation, double refraction of the rays in the ice crystals, and diffraction effects lead to some mixing of the spectral colours. Surprisingly, this makes the arc even more colourful. (A selection of beautiful images you can find at the atmospheric optics site.)
Considering only the vertical plane through the sun, the geometry is much simpler than that of the rainbow. Refraction by a multitude of small prisms floating high up in the atmosphere and directing light from the sun to the observer. To find out that it is a circular arc, however, one needs some algebra. (It is always only part of a circle.)
I have mentioned that the mixing of spectral colours increases the colourfulness. This may sound paradoxical. But compare the two computed arcs below. For faithful rendering of colours a light background has been chosen. |
 |
Left: Under idealized conditions (pointlike sun, exactly oriented, larger ice crystals, no birefringence) the CZA would show pure spectral colours over a relatively bright background.
Right: With realistic assumptions, the pure spectral colours mix, forming a more colourful spectrum with clearly visible "mixed colours" yellow and blue (in contrast to violet-blue seen on the left side).
Parhelia, 22º halo and other arcs

Left parhelion, Hannover, July 20th 2005, 20:19 CEST (solar height 8.7º ).
More pictures
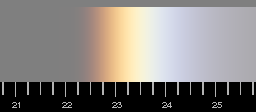 | Colours of the parhelion, computed for 20º solar height and gaussian distribution of tilts with 3º standard deviation (ignoring diffraction effects). The scale below gives the angular distance to the sun.
|
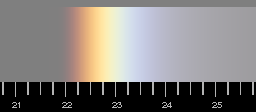 | The same for 15º |
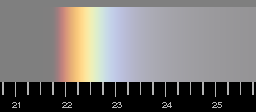 | and for 10º solar height.
|
Some (as I hope) well justified approximations have been done in the calculation. However, in reality, the red side is always more diffuse than the computation shows. This can be explained by diffraction which has not yet been included.
Snow
Colours due to light refraction by ice crystals can also be seen from near by when there is snow and the sun shines. The snow is glittering. Some of the glints are coloured, and the colours change when one is moving. A photograph can only give a rough impression, as the glints are very bright. For enlargement, click on the image!
Photo © Ingrid Pringnitz | |

|
Back to the index page "the origins of colour"
Legal Information Data Privacy